Teoría de las graficas

En matemáticas e informática, la teoría de grafos estudia las propiedades de los gráficos, que son conjuntos de objetos no vacíos llamados vértices o nodos y conjuntos de vértices llamados aristas. Puede o no instruir en inglés. Suele estar representado por una serie de puntos (vértices) conectados por líneas (aristas).

Vértices, Grafos y Subgrafos como definiciones:

Los vértices forman uno de los dos elementos que componen un gráfico. La teoría de grafos, como todas las demás ramas de las matemáticas, no está interesada en saber qué es un vértice. Varias situaciones en las que se pueden identificar objetos y relaciones que cumplen con la definición de un gráfico se pueden ver como gráficos para que se les pueda aplicar la teoría de gráficos.

Un grafo es una pareja de conjuntos G= (V,A), donde V es el conjunto de vértices, y A es el conjunto de aristas, este último es un conjunto de pares de la forma (u,v) tal que u,v ∈ V. En la teoría de grafos, sólo queda lo esencial del dibujo: la forma de las aristas no es relevante, sólo importa a qué vértices están unidas. Además, la ubicación de los puntos de control no importa y se puede cambiar para que el dibujo sea más claro.

Muchas redes cotidianas se pueden modelar gráficamente: la red de carreteras que conectan las ciudades, la red eléctrica o la red de alcantarillado de la ciudad. Un subgrafo de un grafo G es un grafo cuyos conjuntos de vértices y aristas son subconjuntos de los de G. Se dice que un grafo G contiene a otro grafo H si algún subgrafo de G es H o es isomorfo a H (dependiendo de las necesidades de la situación), El subgrafo inducido de G es un subgrafo G’ de G tal que contiene todas las aristas adyacentes al subconjunto de vértices de G.

Diámetro:

En un gráfico, la distancia entre dos vértices es el número mínimo de aristas en el camino entre ellos. En tablas y gráficos, el diámetro es la mayor distancia entre dos puntos de igual valor.

Historia:

La historia de la teoría de grafos comienza con el famoso problema matemático de 1736, Seven Bridges in Russia’s Königsberg Land (ahora Kaliningrado). Leonhard Euler resolvió este problema encontrando un camino a través de los siete puentes del río Pregel de tal manera que todos los puentes estén cubiertos y cada puente se cruce solo una vez. Posteriormente, el 17 de agosto, el físico alemán Gustav Kirchhoff aplicó la teoría de grafos al análisis de redes eléctricas, publicó sus leyes de circuitos y calculó el voltaje y la corriente en un circuito, denominada ley de Kirchhoff, la cual se considera el primer problema técnico que se aplicó la teoría de grafos.

El problema de los cuatro colores:

Luego, el 17 de octubre de 1852, apareció el llamado problema de los cuatro colores, relacionado con la observación del matemático de plantas Francis Guthrie de que los mapas geográficos solo se podían dibujar con cuatro colores, por lo que los países nunca se pintarían de un solo color. En agosto de 1857, el matemático inglés Arthur Cayley investigó y resolvió el problema de enumeración al representar cada compuesto químico como un gráfico, un árbol con vértices que representan átomos y bordes que representan la presencia de enlaces químicos.

En agosto de 1859, el Sr. William Hamilton doce pentágonos (dodecágono) para marcar los nombres de ciudades famosas en veinte nudos, por lo que se creó el juego “La vuelta al mundo”. El juego consiste en encontrar un camino que cruce los vértices exactamente una vez, una línea que los atraviese. En 1936 se publicó el primer libro sobre teoría de grafos, escrito por el matemático húngaro-judío DĕNES KÖNIG. Se puede decir que este libro es el comienzo de la teoría de grafos moderna. En 1977, los matemáticos Kenneth Apel y Wolfgang Hacken encontraron una forma de resolver este problema, y ​​un siglo después puede considerarse el nacimiento de la teoría de grafos. Para aclarar esto, los matemáticos han definido los términos y conceptos básicos de la teoría de grafos.

Estructuras de Datos en la Representación de Grafos:

Hay varias formas de guardar gráficos en su computadora. La estructura de datos utilizada depende de las características del gráfico y de los algoritmos utilizados para procesarlo. Las estructuras más simples y más utilizadas son las listas y las matrices, aunque a menudo se utilizan combinaciones de las dos. Las listas se prefieren en gráficos dispersos porque son eficientes en memoria. Por otro lado, las matrices brindan un acceso rápido, pero usan mucha memoria.

Estructura de Lista:

• lista de incidencia: Las aristas son representadas con un vector de pares (ordenados, si el grafo es dirigido), donde cada par representa una de las aristas.

 • lista de adyacencia: Cada vértice tiene una lista de vértices los cuales son adyacentes a él. Esto causa redundancia en un grafo no dirigido (ya que A existe en la lista de adyacencia de B y viceversa), pero las búsquedas son más rápidas, al costo de almacenamiento extra.

En esta estructura de datos la idea es asociar a cada vértice i del grafo una lista que contenga todos aquellos vértices j que sean adyacentes a él. De esta forma sólo reservará memoria para los arcos adyacentes a i y no para todos los posibles arcos que pudieran tener como origen i. El grafo, por tanto, se representa por medio de un vector de n componentes (si |V|=n) donde cada componente va a ser una lista de adyacencia correspondiente a cada uno de los vértices del grafo. Cada elemento de la lista consta de un campo indicando el vértice adyacente. En caso de que el grafo sea etiquetado, habrá que añadir un segundo campo para mostrar el valor de la etiqueta.

Estructuras matriciales:

• Matriz de incidencia: El grafo está representado por una matriz de A (aristas) por V (vértices), donde [arista, vértice] contiene la información de la arista (1 – conectado, 0 – no conectado)

 • Matriz de adyacencia:  El grafo está representado por una matriz cuadrada M de tamaño n², donde n es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento m_xy es 1, de lo contrario, es 0.

Aristas dirigidas y no dirigidas

 En algunos casos es necesario asignar un sentido a las aristas, por ejemplo, si se quiere representar la red de las calles de una ciudad con sus direcciones únicas. El conjunto de aristas será ahora un subconjunto de todos los posibles pares ordenados de vértices, con (a, b) ≠ (b, a). Los grafos que contienen aristas dirigidas se denominan grafos orientados o dirigidos. Las aristas no orientadas se consideran bidireccionales para efectos prácticos (equivale a decir que existen dos aristas orientadas entre los nodos, cada una en un sentido).

Caracterización de Grafos:

Grafos simples:

Un grafo es simple si a lo más existe una arista uniendo dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos. Un grafo que no es simple se denomina multígrafo.

Grafos conexos:

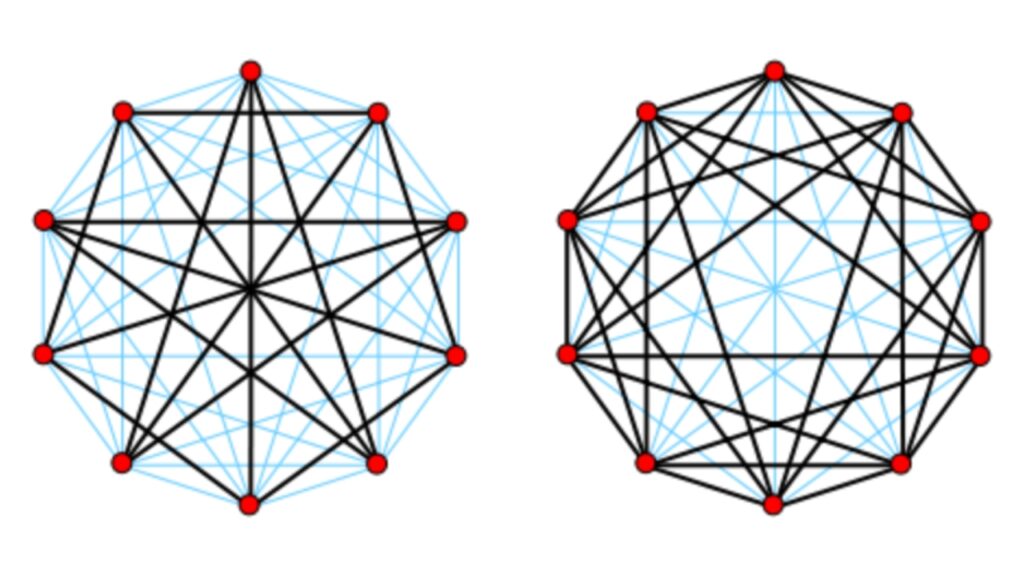
Un grafo es conexo (figura de la izquierda) si cada par de vértices está conectado por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde a hacia b. Un grafo es doblemente conexo si cada par de vértices está conectado por al menos dos caminos disjuntos; es decir, es conexo y no existe un vértice tal que al sacarlo el grafo resultante sea disconexo o no conexo (figura de la derecha).

En términos matemáticos la propiedad de un grafo de ser conexo permite establecer con base en él una relación de equivalencia para sus vértices, la cual lleva a una partición de éstos en “componentes conexas”, es decir, porciones del grafo, que son conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

Grafos completos:

Un grafo es completo si existen aristas uniendo todos los pares posibles de vértices. Es decir, todo par de vértices (a, b) debe tener una arista e que los une. El conjunto de los grafos completos es denominado usualmente K, siendo K_n el grafo completo de n vértices. Un K_n, es decir, grafo completo de vértices tiene exactamente n(n-1)/2 aristas. La representación gráfica de los K_n como los vértices de un polígono regular da cuenta de su peculiar estructura.

Grafos bipartitos:

Un grafo G es bipartito si puede expresarse como G=(V1 U V2, A) es decir, sus vértices son la unión de dos grupos de vértices, bajo las siguientes condiciones:

1. V1 y V2 son disjuntos y no vacíos.
2. Cada arista de A une un vértice de V1 con uno de V2 .
3. No existen aristas uniendo dos elementos de V1 ; análogamente para V2 .

Bajo estas condiciones, el grafo se considera bipartito, y puede describirse informalmente como el grafo que une o relaciona dos conjuntos de elementos diferentes, como aquellos resultantes de los ejercicios y puzzles en los que debe unirse un elemento de la columna A con un elemento de la columna B.

Videos complementarios:

Profe Christian Staple (11 de octubre de 2021) Grafos completo . YouTube https://www.youtube.com/watch?v=ElRsxnYpWaQ

Créditos:

Autor: Dikson Javier Castillo Triviño

Editor: Master Carlos Iván Pinzón Romero

Código: UCPSG7-1

Universidad: Universidad Central

Fuentes:

Profe Christian Staple (11 de octubre de 2021) Grafos completo . YouTube https://www.youtube.com/watch?v=ElRsxnYpWaQ
ParaDoppler (26 de mayo de 2021) El maravilloso mundo de la Teoría de Grafos . YouTube.  https://www.youtube.com/watch?v=mZMJJV6jDec
Pedro Alexis () Historia De La Teoria De Los Grafos. TimeToast. https://www.timetoast.com/timelines/historia-de-la-teoria-de-los-grafos
Teoría de grafos. (15 de febrero de 2023). En Wikipedia. https://es.wikipedia.org/wiki/Teor%C3%ADa_de_grafos
http://ebadillo_computacion.tripod.com/teoria_de_graficas.pdf
Teoría de grafos. En Libroz.com. https://www.unipamplona.edu.co/unipamplona/portalIG/home_23/recursos/general/11072012/grafo3.pdf
Teoría de grafos. (15 de febrero de 2023). En Wikipedia.  https://upload.wikimedia.org/wikipedia/commons/thumb/6/65/Connexe_et_pas_connexe.svg/400px-Connexe_et_pas_connexe.svg.png
Blanca Nayelly Del Castillo Velasco Martínez (08 de diciembre de 2016). El problema de los cuatro colores. revistac2. https://www.revistac2.com/el-problema-de-los-cuatro-colores/
Revistac2. (2016). World Map [imagen]. https://www.revistac2.com/c2/wp-content/uploads/2016/12/world_map.png
eralvana. (2020). Teoria de graficas [imagen]. https://www.google.com/imgres?imgurl=https%3A%2F%2Feralvana.github.io%2FCursosUNAM%2F2020-2%2Ftg%2Fimg-video%2FPetersen-complement.png&imgrefurl=https%3A%2F%2Feralvana.github.io%2FCursosUNAM%2F2020-2%2Ftg%2Findex.html&tbnid=ghwKsCVwNSOZ_M&vet=12ahUKEwjrvb6FiND9AhVJcjABHZ7tAQ4QMygAegUIARCNAQ..i&docid=k0D5gJxTpKBTMM&w=450&h=220&q=teor%C3%ADa%20de%20las%20gr%C3%A1ficas%20&ved=2ahUKEwjrvb6FiND9AhVJcjABHZ7tAQ4QMygAegUIARCNAQ