Rotación: Ángulos de Euler y Cuaterniones
En diferentes campos de la tecnología es necesario realizar rotación de imágenes. Desde el desarrollo de videojuegos hasta el lanzamiento de satélites al espacio requieren la comprensión del concepto de rotación. En este artículo se abordará la rotación usando los ángulos de Euler, qué limitaciones tiene esta técnica y cómo los cuaterniones son la elección de preferencia para la implementación de algoritmos de computación que calculen rotaciones.
Rotación
La rotación es un concepto matemático que viene de la geometría. Todo movimiento definido en un plano (2D) o un espacio (3D) que conserva al menos un punto en la posición original, es una rotación. La rotación también se puede considerar para espacios n-dimensionales.
Matriz de Rotación
Una matriz de rotación es aquella que representa una rotación en el espacio euclídeo. Este concepto proviene del álgebra lineal.
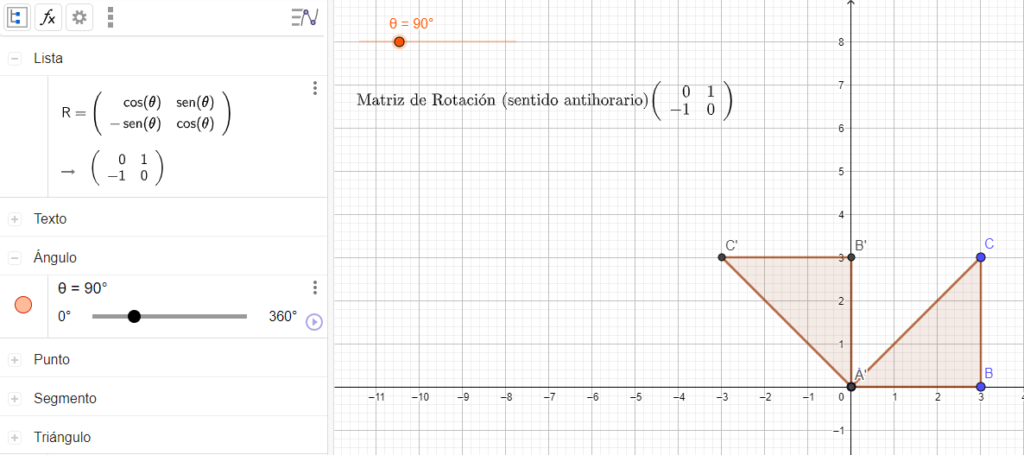
La matriz R representa la rotación de θ grados. En la gráfica anterior vemos como el triángulo ABC rota 90° sobre A, transformándolo en el triángulo en A’B’C’.
Ángulos de Euler
Los ángulos de Euler son un conjunto de tres coordenadas que indican la orientación de un sistema de referencia con respecto a otro sistema de referencia en el cual uno de ellos es fijo y el otro el móvil.
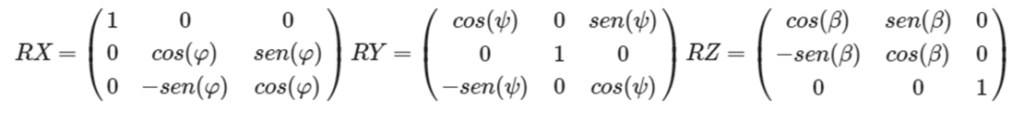
En un sistema ortonormal XYZ se define una matriz de rotación por cada uno de los ejes. Como se puede observar se tienen tres ángulos que indican la rotación para cada eje.
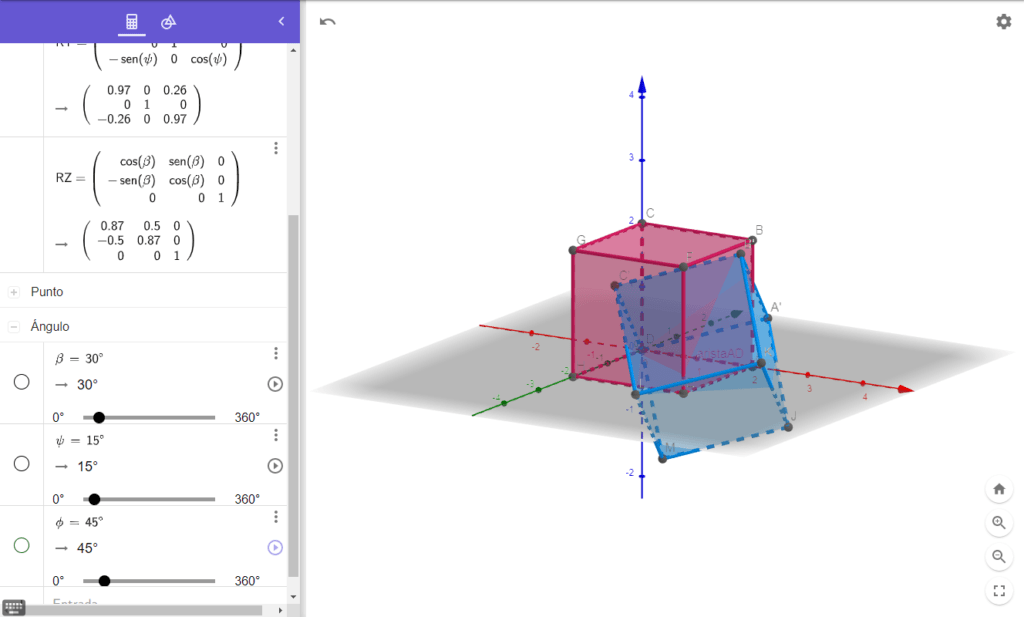
En el ejemplo anterior se está haciendo una rotación del cubo sobre los diferentes ejes, 45°, 15° y 30° respectivamente.
Bloqueo del cardán – Gimbal lock
El bloqueo del cardán se presenta cuando se pierde un grado de libertad debido a la alineación de dos ejes, generando así un bloqueo en uno de los ejes. Por ejemplo, al rotar el cubo en el eje Y 90°, se pierde libertad para girar sobre el eje X ya que al tratar de rotar sobre X se observa que la figura rota sobre el eje Z.
Rotación con Cuaterniones
Un cuaternión es una extensión de los números reales de la forma q = w + xi + yj + zk siendo w, x, y, z números reales y i, j, k números imaginarios que cumplen la siguiente condición i2 = j2 = k2 = ijk = -1.
A través de la multiplicación de números complejos se pueden hacer rotaciones en el plano 2D usando la fórmula de Euler para involucrar el ángulo. Así mismo la multiplicación de cuaterniones permite hacer rotaciones en el plano 3D.
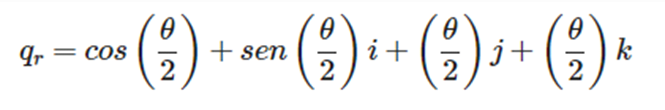
Para rotar Ɵ grados alrededor de un eje se multiplica por el cuaternión qr.
Para profundizar sobre el tema se recomienda ver el siguiente video.
Autor: Carlos Alberto Trujillo
Editor: Carlos Pinzón
Código: UCRV-4
Universidad: Universidad Central
Fuentes:
Nazarala, H. (31 de julio de 2019). Unity: Tutorial Quaternion Basico en Español! [Video]. YouTube. https://www.youtube.com/watch?v=B58A1qkEkik
Rotación (matemáticas). (2020, 16 de octubre). En Wikipedia. https://es.wikipedia.org/wiki/Rotaci%C3%B3n_(matem%C3%A1ticas)
Matriz de rotación. (2020, 4 de octubre). En Wikipedia. https://es.wikipedia.org/wiki/Matriz_de_rotaci%C3%B3n
Ángulos de Euler. (2020, 13 de abril). En Wikipedia. https://es.wikipedia.org/wiki/%C3%81ngulos_de_Euler
Cuaternión. (2020, 12 de agosto). En Wikipedia. https://es.wikipedia.org/wiki/Cuaterni%C3%B3n
Trujillo, C. (2020). Rotación en 3D. Geogebra. https://www.geogebra.org/m/kneqysnj
Trujillo, C. (2020). Rotación en 2D. Geogebra. https://www.geogebra.org/m/z6rsq29a
Altmann, G. (2015). Geometría Matemáticas Cubo. [Fotografía]. Pixabay. https://pixabay.com/es/illustrations/geometr%C3%ADa-matem%C3%A1ticas-cubo-hexaedro-1023846/


Muchas gracias por tu aportación. Feliz semana.