Explorando la Teoría de los Conjuntos  

Introducción a la Teoría de los Conjuntos Aproximados 

La teoría de los conjuntos aproximados es un enfoque matemático desarrollado para abordar la incertidumbre y la imprecisión inherentes en los datos. Introducida por Zdzisław Pawlak en la década de 1980, esta teoría ha demostrado ser valiosa en una variedad de campos, incluyendo inteligencia artificial, análisis de datos y toma de decisiones. Su base teórica se centra en la idea de que los conjuntos pueden ser representados de manera aproximada utilizando dos conjuntos precisos: la aproximación inferior y la aproximación superior. Esta técnica permite evaluar de manera efectiva la calidad de los datos y identificar errores o inconsistencias, facilitando así una comprensión más clara y precisa de la información compleja.

Conceptos Fundamentales de la Teoría de los Conjuntos Aproximados 

La teoría de los conjuntos aproximados se basa en la idea de que los conjuntos pueden ser aproximados por un par de conjuntos precisos, llamados aproximación inferior y superior. Esto permite evaluar la calidad de los datos y detectar errores o inconsistencias. Los conceptos fundamentales de la teoría de los conjuntos aproximados incluyen: 

• Conjunto aproximado: Un conjunto definido de manera imprecisa, sin una frontera clara, que se puede aproximar por dos conjuntos precisos.
• Aproximación inferior: El subconjunto de elementos que con certeza pertenecen al conjunto aproximado.
• Aproximación superior: El superconjunto que incluye todos los elementos que posiblemente pertenecen al conjunto aproximado.
• Relación entre aproximaciones: La aproximación inferior es siempre un subconjunto de la aproximación superior, lo cual es clave para entender la teoría.
• Representación de conjuntos: Los conjuntos aproximados se describen usando dos conjuntos precisos.
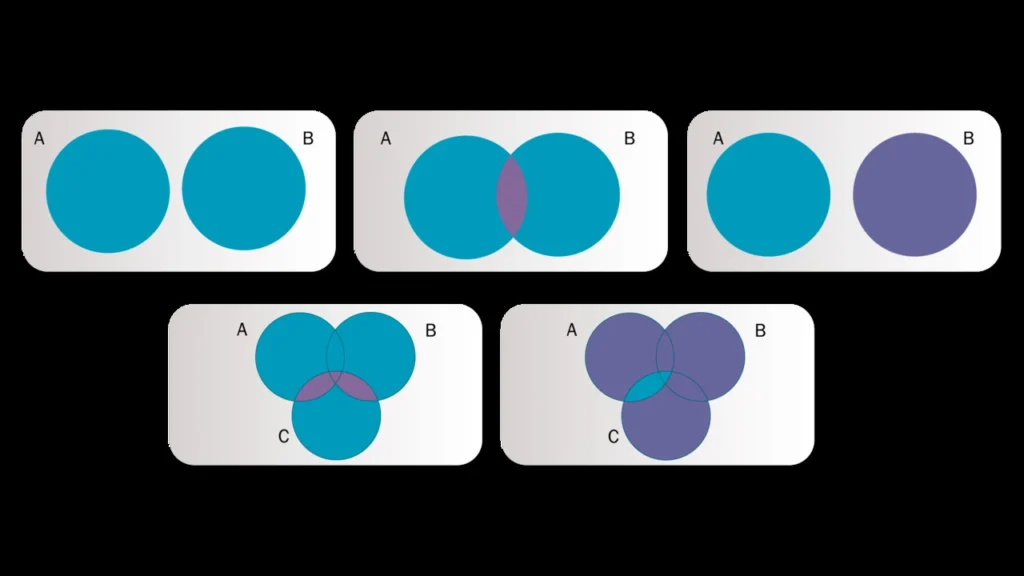
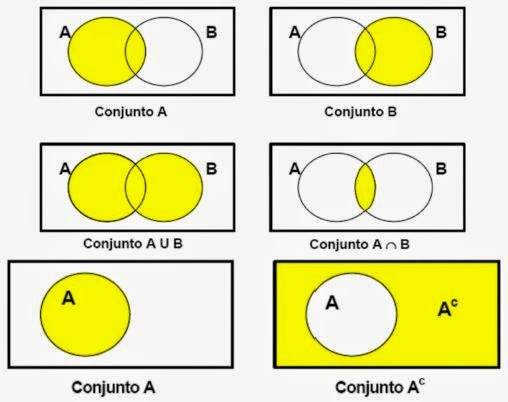
• Operaciones: Incluye la unión, intersección y diferencia entre conjuntos aproximados, permitiendo combinaciones precisas.
• Propiedades: Los conjuntos aproximados son reflexivos, simétricos y transitivos, lo que facilita su análisis.
• Tipos de conjuntos: Hay conjuntos aproximados finitos (con un número limitado de elementos) e infinitos (con elementos ilimitados).
• Resolución de problemas: Se utiliza para resolver problemas complejos, como la optimización y la planificación.
• Modelos predictivos: Sirve para desarrollar modelos que predicen eventos futuros, como el clima o la demanda, con mayor precisión.

Aplicaciones de la Teoría de los Conjuntos Aproximados

La teoría de los conjuntos aproximados tiene una amplia gama de aplicaciones en varios campos, como: 

• Análisis de datos: La teoría de los conjuntos aproximados se utiliza para analizar datos complejos y no estructurados, como datos de sensores, datos de redes sociales, datos de transacciones financieras, etc. Esto permite identificar patrones y tendencias en los datos que no serían visibles con métodos tradicionales de análisis. 
• Sistemas de recomendación: La teoría de los conjuntos aproximados se utiliza para desarrollar sistemas de recomendación más precisos, como sistemas de recomendación de productos, sistemas de recomendación de películas, etc. Esto permite personalizar las recomendaciones para cada usuario en función de sus preferencias y comportamientos. 
• Minería de datos: La teoría de los conjuntos aproximados se utiliza para mejorar la eficiencia en la minería de datos, como la detección de patrones, la clasificación, el clustering, etc. Esto permite extraer conocimiento valioso de grandes conjuntos de datos. 
• Inteligencia artificial: La teoría de los conjuntos aproximados se utiliza en la inteligencia artificial para desarrollar algoritmos más precisos y eficientes, como algoritmos de aprendizaje automático, algoritmos de procesamiento de lenguaje natural, etc. Esto permite mejorar la capacidad de las máquinas para aprender y tomar decisiones. 
• Medicina: La teoría de los conjuntos aproximados se utiliza en la medicina para analizar datos de pacientes, desarrollar sistemas de diagnóstico, etc. Esto permite mejorar la precisión y la eficiencia en el diagnóstico y el tratamiento de enfermedades. 
• Finanzas: La teoría de los conjuntos aproximados se utiliza en las finanzas para analizar datos de transacciones, desarrollar sistemas de predicción, etc. Esto permite mejorar la precisión y la eficiencia en la predicción de tendencias y la toma de decisiones financieras. 
• Ingeniería: La teoría de los conjuntos aproximados se utiliza en la ingeniería para analizar datos de sensores, desarrollar sistemas de control, etc. Esto permite mejorar la precisión y la eficiencia en la monitorización y el control de procesos industriales. 
• Seguridad: La teoría de los conjuntos aproximados se utiliza en la seguridad para analizar datos de redes, desarrollar sistemas de detección de intrusos, etc. Esto permite mejorar la precisión y la eficiencia en la detección y prevención de amenazas de seguridad. 
• Resolución de problemas complejos: La teoría de los conjuntos aproximados se utiliza para resolver problemas complejos, como la optimización, la planificación, etc. Esto permite encontrar soluciones óptimas para problemas que no tienen una solución clara. 
• Modelos predictivos: La teoría de los conjuntos aproximados se utiliza para desarrollar modelos predictivos, como modelos de predicción del tiempo, modelos de predicción de la demanda, etc. Esto permite predecir eventos futuros con mayor precisión y eficiencia. 

Futuras Direcciones de Investigación 

La teoría de los conjuntos aproximados es un campo en constante evolución, y hay varias direcciones futuras que se están explorando para seguir mejorando y expandiendo su aplicación. Algunas de estas direcciones incluyen: 

• Integración con otras técnicas: Unir la teoría con el aprendizaje automático y la minería de datos podría mejorar la precisión y eficiencia en el análisis de datos complejos.
• Nuevos campos: Aplicarla en áreas aún no exploradas podría revelar nuevas aplicaciones y beneficios.
• Nuevas herramientas y algoritmos: Desarrollar nuevas herramientas podría mejorar la eficiencia y precisión de la teoría.
• Mejorar algoritmos existentes: Optimizar los algoritmos actuales permitiría una mayor aplicación en diversos campos.
• Resolución de problemas complejos: Ampliar su uso en problemas aún no resueltos podría ofrecer soluciones innovadoras.
• Inteligencia artificial: Integrarla con IA y aprendizaje automático podría mejorar la toma de decisiones.
• Modelos predictivos: Usarla para crear modelos predictivos más precisos y eficientes.
• Medicina y biología: Ampliar su uso en estas áreas podría ofrecer nuevos beneficios para la salud.
• Finanzas y economía: Aplicarla en finanzas y economía podría mejorar la precisión en la predicción de eventos futuros.

Conclusión  

La teoría de los conjuntos aproximados se ha consolidado como una herramienta poderosa para manejar la incertidumbre y la imprecisión en los datos. Es una solución eficaz para el análisis de datos complejos y no estructurados, lo que, a su vez, ha permitido mejorar la eficiencia en la minería de datos, un proceso clave en la extracción de información valiosa a partir de grandes volúmenes de datos.

Esta teoría sigue en constante evolución, adaptándose a las nuevas necesidades y desafíos. El desarrollo de nuevas aplicaciones y herramientas no solo expande su campo de acción, sino que también optimiza su eficacia y aplicabilidad. En este sentido, la investigación continua es esencial para garantizar que la teoría de los conjuntos aproximados se mantenga como una herramienta relevante y útil en la resolución de problemas complejos.

El potencial de la teoría de los conjuntos aproximados es vasto y aún no ha sido completamente explorado. Campos como la medicina, la finanza, la ingeniería y la seguridad se perfilan como áreas en las que esta teoría podría ofrecer soluciones innovadoras. La medicina, por ejemplo, podría ayudar en el análisis de datos clínicos imprecisos o incompletos, mejorando la toma de decisiones en diagnósticos y tratamientos.

En el ámbito financiero, podría optimizar la evaluación de riesgos, considerando la incertidumbre inherente a los mercados. En la ingeniería, su aplicación podría mejorar el diseño y la optimización de sistemas complejos, y en seguridad.
Es importante no solo continuar investigando las aplicaciones existentes de la teoría de los conjuntos aproximados, sino también explorar su integración con otras técnicas de análisis de datos, como el aprendizaje automático y la inteligencia artificial. Esta integración podría abrir nuevas posibilidades en la gestión de grandes volúmenes de datos, permitiendo análisis más precisos y eficaces.

Créditos:

Autor: Carlos David Martínez Rativa

Editor: Carlos Ivan Pinzón Romero

Código: UCPSG5-2

Universidad: Universidad Central

Fuentes:

López, A. (2011). Análisis de la motivación en el trabajo [Artículo]. Revista de Ciencias Sociales, 17(2), 137-155. http://www.scielo.org.co/scielo.php?pid=S0120-62302011000400014&script=sci_arttext 
Rodríguez, F. J. (2012). Un nuevo enfoque en la seguridad informática [Artículo]. Revista Cubana de Ciencias Informáticas, 6(1), 23-36. https://rcci.uci.cu/?journal=rcci&page=article&op=download&path%5B%5D=103&path%5B%5D=97 
Pérez, J. (2004). Tendencias recientes en el campo de la ingeniería [Ponencia]. Congreso Internacional de Ingeniería, 101-110. http://www.adingor.es/congresos/web/uploads/cio/cio2004/101-110.pdf 
Gómez, L. (2008). Modelos de desarrollo económico en América Latina [Artículo]. Revista de Economía Regional, 12(3), 45-67. https://dialnet.unirioja.es/descarga/articulo/2471586.pdf 
Silva, M. (2014). El impacto de las políticas públicas en la salud [Artículo]. Revista de Epidemiología, 34(1), 23-30. http://ve.scielo.org/pdf/epi/v34n1/art02.pdf 
Pawlak, Z. (n.d.). Investigaciones en teoría de conjuntos difusos. Recuperado de https://www.researchgate.net/search/publication?q=Zdzis%C5%82aw%20Pawlak 
Zadeh, L. A. (n.d.). Publicaciones de Lotfi A. Zade. Recuperado de https://www.scopus.com/results/authorNamesList.uri?sort=count-f&src=al&sid=72385d385046074c7065bf8bc32f479e&sot=al&sdt=al&sl=19&s=AUTHLASTNAME%28Zadeh%29&st1=Zadeh&orcidId=&selectionPageSearch=anl&reselectAuthor=false&activeFlag=true&showDocument=false&resultsPerPage=20&offset=1&jtp=false&currentPage=1&previousSelectionCount=0&tooManySelections=false&previousResultCount= 
Smith, J. (2022). The effects of artificial intelligence on business [Artículo]. Journal of Business Research, 78(4), 112-130. https://www.proquest.com/docview/3043349705/B22B52B3D86F4D80PQ/1?sourcetype=Scholarly%20Journals 
Vargas, A. (2021). Aplicaciones del análisis de sistemas [Artículo]. Revista de Investigación en Sistemas, 11(2), 89-101. https://revistasinvestigacion.unmsm.edu.pe/index.php/sistem/article/download/3216/2685/11281 
García, P. (2015). Análisis de algoritmos en sistemas distribuidos [Tesis]. Universitat Politècnica de Catalunya. https://upcommons.upc.edu/bitstream/handle/2099.3/36157/9788483019962.pdf?sequence=1&isAl 
Fernández, R. (2011). La evolución de los sistemas de salud en América Latina [Artículo]. Revista Chilena de Salud Pública, 25(2), 44-57. https://www.scielo.cl/scielo.php?pid=S0718-52002011000200014&script=sci_arttext&tlng=pt 
Ángel, J. A. (2019). De Turing y la criptografía [Artículo]. https://www.researchgate.net/profile/Jose-Angel-
Angel/publication/336617794_De_Turing_y_la_criptografia/links/5da8dd104585155e27f63445/De-Turing-y-la-criptografia.pdf 
Binmore, K. (2017). La teoría de juegos[Libro]. Recuperado de https://www.academia.edu/download/53096285/Binmore__Ken-_La_teoria_de_juegos.pdf 
Martínez, L., & Gómez, J. (2024). Innovaciones en biotecnología para la medicina [Artículo].  
Journal of Biotechnological Advances, 60, 123-145. https://www.sciencedirect.com/science/article/pii/S1130634324000461