La teoría de conjuntos: Fundamentos y aplicaciones

La teoría de conjuntos es una de las bases fundamentales en la matemática moderna la cual es usada para establecer bases en la formulación de problemas en diversas áreas de la matemática desde lógica matemática, informática, física y hasta la economía. 

La desarrolló el matemático Alemán Georg Cantor a finales del siglo XIX. Este nos ha ayudado a evolucionar la forma en como vemos, entendemos y abordamos problemas matemáticos entre muchos otros campos. En este artículo se explorará las bases de la teoría de conjuntos sus aplicaciones, historia y algunas de sus aplicaciones más relevantes 

Definición

La teoría de conjuntos una de las ramas de la matemática y de la lógica la cual se dedica a estudiar las características de los conjuntos y las operaciones que se realizan entre los mismos. 

En su configuración básica un conjunto es una agrupación bien definida de objetos, llamados elementos los cuales comparten alguna característica en común. Por ejemplo, los números naturales menores de 8 se representan como {1, 2, 3, 4, 5, 6, 7, 8,}, en la teoría de conjuntos los conjuntos se representan con llaves {}, y los elementos dentro de ellos van separados por comas. 

Así mismo la teoría se enfoca en estudiar los conjuntos, en esto se encuentran sus atributos, las relaciones que pueden establecer entre ellos. ya sean la unión, intersección. complemento u otros, para definir un conjunto se buscar la característica que tienen en común sus elementos. Por ejemplo, un conjunto Z con números enteros positivos y pares menores que 1000. 

Ejemplos  

La colección de letras de la palabra “musculo”. 

La agrupación de números primos entre 0 y 20. A={2,3,5,7,11,13,17,19}

Aplicaciones  

La teoría de conjuntos tiene una gran variedad de aplicaciones en diversos campos del conocimiento. 

Algunas de las áreas donde se aplican son: 

• Matemática pura: La teoría de conjuntos nos otorga las herramientas necesarias para formular y solucionar los problemas que se llegan a plantear en áreas como el algebra, cálculo, geometría, estadística, trigonometría y la teoría de números. 
• Lógica matemática: En lógica matemática La teoría de conjuntos es una herramienta fundamental en el estudio de la lógica matemática en particular la construcción de sistemas formales especialmente porque estos buscan capturar y extraer características determinadas del mundo real en un modelo conceptual y demostración de teoremas. 
• Informática: La teoría de conjuntos en informática se usa para la teoría de computación, inteligencia artificial, esto mediante la organización de variables en determinados grupos con una naturaleza similar también en el diseño y análisis de algoritmos de manera que puede dar una orden mediante la organización de varias partes con una característica en común. 
• Estadística y probabilidad: En estadística y probabilidad la teoría de conjuntos se usa para agrupar variables que pueden compartir alguna propiedad en común las cuales ayudan a prevenir los cambios que estas pueden llegar a tener, también nos ayudan a analizar datos o eventos con cierto grado de aleatoriedad. 
• Física, Ciencias y Naturales: La teoría de conjuntos aplica a la hora de formular teorías físicas, en como agrupamos a los fenómenos naturales, también son aplicados en la mecánica cuántica y la teoría de la relatividad. 
• Economía y ciencias sociales: En economía y ciencias sociales usamos la teoría de conjuntos en modelización de preferencias, la teoría de juegos y toma de decisiones. 

Bases de los conjuntos   

Cuando hablamos de las operaciones básicas en la teoría de conjuntos nos referimos a la diferencia, intersección, la diferencia simétrica y complemento. 

• Unión: La unión en conjuntos se refiere a la sumatoria de los elementos que pertenecen a ambos conjuntos como, por ejemplo: los conjuntos A y B denotada como A ∪ B. En este caso el conjunto A tiene todos los números pares menores que 100 y el conjunto B tiene todos los números reales cuya suma da menos de 1000 por que se referiría a juntar todos los elementos de A y B. 
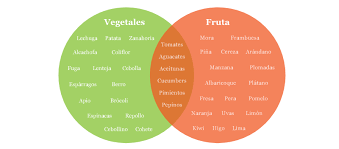
• Intersección: La intersección en conjuntos se refiere a los elementos que tienen en común dos conjuntos no vacíos en este caso los conjuntos A y B denotada como A ∩ B es el conjunto que contiene los elementos que estos tienen en común 
• Diferencia: Cuando hablamos de la diferencia en la teoría de conjuntos nos referimos a los elementos que están en el conjunto A, pero no en el conjunto B esto lo representamos de la siguiente forma A-B o A/B. 
• Complemento: Cuando hablamos de complemento en conjuntos nos referimos a los elementos del conjunto u (universal) que no están en el conjunto A se puede denotar de la siguiente forma A^c o A’. 

Conjuntos Especiales 

• Conjuntos Especiales: Existen muchos tipos de conjuntos especiales los cuales juegan un papel fundamental en la teoría de conjuntos tal como lo pueden ser los axiomas. 
• Conjunto Vacío: Cuando hablamos de un conjunto vacío nos referimos a uno el cual no tiene ningún elemento y se puede denotar de la siguiente forma. 
• Conjunto universal: Cuando hablamos del conjunto universal no referimos a un conjunto el cual tiene todos los elementos en el cual aplica un contexto en específico y se puede denotar de la siguiente manera  
• Conjunto Disjunto: Cuando hablamos de conjuntos disjuntos nos referimos a dos conjuntos los cuales no tienen elementos en común, es decir su intersección no tiene ningún elemento. 

Simbología en conjuntos

Axiomas  

Cuando hablamos de axiomas nos referimos a principios o teorías que se admiten sin alguna demostración debido a lo claro u obvios que son, la teoría de conjuntos establece unas reglas fundamentales para el uso de conjuntos, algunos de los más importantes son: 

• Axioma de Extensionalidad: Esto se refiere a dos conjuntos que son iguales solo si tienen los mismos elementos  
• Axioma de separación: Dada una propiedad, se pueden formar un conjunto que contenga todos los elementos que se acoplen a una característica en especifico  
• Axioma de la existencia del conjunto vacío: Esta habla del conjunto vacío, este como dice el nombre no contiene ningún elemento. 

conclusión  

La teoría de conjuntos es una herramienta que nos acompaña hasta el día de hoy la cual a ido evolucionando con el pasar de los años con los diferentes aportes que se le han hecho con el pasar del tiempo, los conjuntos son usados para el planteamiento de problemas en casi todas las áreas del conocimiento refiriéndonos a las matemáticas y demás en todo esto podemos ver que los conjuntos son usados para la agrupación de términos conceptos y demás también se puede ver como la teoría influye en las áreas del conocimiento y como ha ayudado a evolucionar a las mismas 

Autor: Sebastián Soriano G

Editor:

Código: UCPS-1

Universidad: Universidad Central

Fuentes

Fuentes: 

Ivorra C. (1999). Lógica y teoría de conjuntos. https://paca.ime.usp.br/pluginfile.php/19778/mod_resource/content/0/Listas_de_exercicios/Logica.pdf  

Ivorra C. (2008). La Axiomática en la teoría de conjuntos. https://www.uv.es/Ivorra/Libros/Axiomas.pdf  

Fernando Hernández (2003). Teoría de conjuntos. https://acortar.link/lPn94W  

Canal CIS3. (17 de junio de 2020) Historia y Conceptos básicos de la teoría de conjuntos. https://youtu.be/nQbEIDqvftY 

https://matematicasdiscretas.org/simbologia-de-teoria-de-conjuntos/  

Diagrama de Venn. https://datavizcatalogue.com/ES/metodos/images/top_images/SVG/diagrama_de_venn.svg 

Adaptado de Georg Ferdinand. Por ECURED. https://www.ecured.cu/images/8/8d/Georg_Ferdinand.jpg  

Adaptado de Geometría Matemáticas. De Gerald (4 de noviembre de 2015). https://cdn.pixabay.com/photo/2015/11/05/08/21/geometry-1023846_1280.jpg Licencia de contenido