Teoría de los grafos ¿Se relaciona con la TGS? 

¿Qué es una gráfica?: 

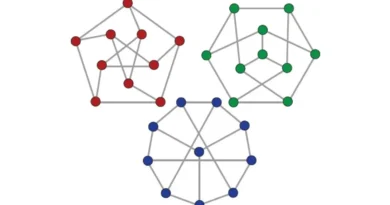
Un grafo (o una gráfica) son cuerpos formados por nodos y vértices, los cuales forman conexiones entre sí, llamadas aristas. Los grafos son usados en el ámbito de la matemática y en la computación para estudiar las relaciones que existen entre unidades que interactúan con otras.

Son necesariamente útiles en estos dos campos de estudio, ya que permiten una mayor facilidad para poder representar diversas situaciones o elementos, como por ejemplo en el análisis de datos estadísticos (esto relacionado en el ámbito de la matemática) y también en las redes de computadoras, ya que en este ámbito los vértices representan terminales y las aristas conexiones, las cuales pueden ser representadas por cables o conexiones inalámbricas  

Su historia:  

El inicio de esta teoría data del año 1736 cuando se originó el famoso problema matemático de “Los puentes de Königsberg”, este problema fue resuelto por Leonhard Euler, que, gracias a su solución, le dio origen a esta teoría. Este mismo concluyó que no era posible solucionar este problema, ya que en el contexto del problema no se podía hallar un camino posible para el mismo. 

Para el año 1847, el físico alemán Gustav Kirchhoff dio origen a sus leyes físicas, más conocidas como “Leyes de Kirchhoff”. Lo hizo basándose en la teoría de los grafos, la cual, a su vez, aplicó a su análisis de redes eléctricas, que también, a su vez, hizo que publicara sus leyes de circuitos y, además, calculó el voltaje y la corriente, todo esto basado en la teoría de los grafos. 

En 1857 surge el llamado “Problema de los isómeros” por Arthur Cayley, el cual investigó y solucionó él mismo, asignándole a cada elemento químico un árbol (es decir, un grafo). Ese árbol estaba conformado por puntos y aristas, en donde, los puntos representaban cada átomo y las aristas representaban la presencia de enlaces químicos 

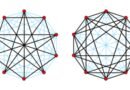
Sir. William Hamilton fue un matemático británico, el cual, en el año 1859, creó un pasatiempo matemático que, hoy en día, sigue siendo utilizado, el cual se llamaba: “Icosian Game” (o Alrededor del mundo). Para crear este pasatiempo, tuvo como base a un dodecaedro (una figura de 12 caras) y le agregó 20 puntos con un simple objetivo: Encontrar un camino que recorra los 20 vértices solo una vez 

Hasta el año 1884 se empezó a usar el término “grafo” para darle nombre a esta teoría. Quien empleó ese término por primera vez (indirectamente) fue el químico inglés Edward Frankland (la llamaba “notación gráfica”), hasta que el químico orgánico escocés Alexander Crum Brown definió el término “grafo” definitivamente, ya que, para él, un grafo era la representación gráfica de los enlaces entre los átomos de una molécula. 

En el siglo XX (exactamente en el año 1936) el matemático húngaro Dénes Kőnig lanzó el primer libro relacionado con la teoría de los grafos, el cual, hasta la fecha, es considerado el promotor de la teoría de los grafos moderna. 

El problema de los cuatro colores: 

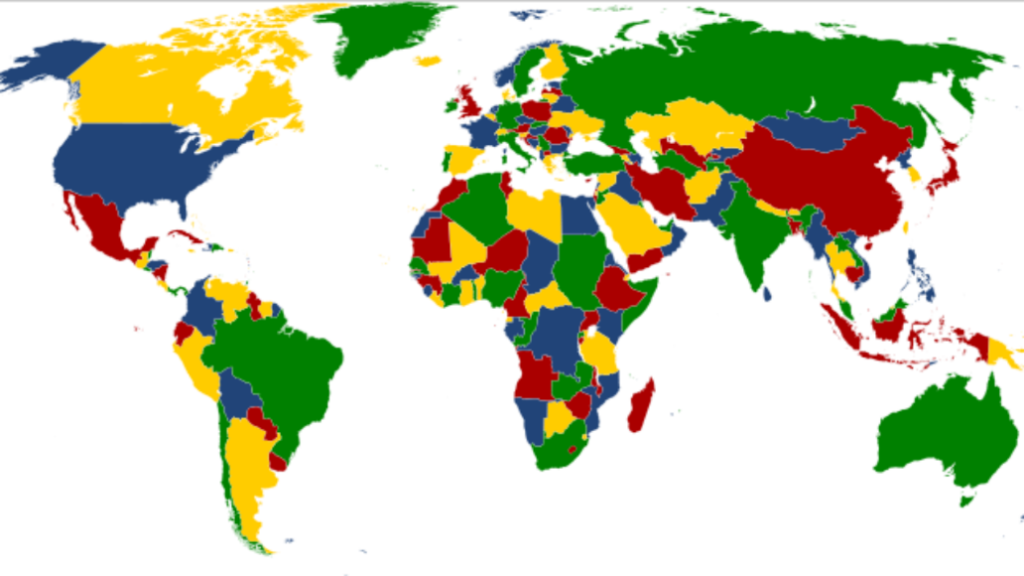
Para el año 1852, el matemático inglés Francis Guthrie planteó un reconocido problema: El problema de los cuatro colores. Este problema tenía una pregunta clave, planteada por el mismo Francis: “¿Es posible pintar cualquier mapa de países con solo cuatro colores?”, es decir, colorear un mapamundi con una pequeña condición: Dos países vecinos NO podían tener el mismo color. 

Más de un siglo después (para ser exactos, 125 años después), en el año 1977, los matemáticos Kenneth Appel y Wolfgang Haken (estadounidense y alemán, respectivamente) lograron resolver entre los dos el problema de los cuatro colores propuesto por Francis Guthrie, el cual, al principio, no era bien recibido por la comunidad matemática dada a su rara demostración, ya que fue resuelto con la ayuda de un ordenador, lo cual hizo que tuviera una cantidad exagerada de pequeños detalles, lo que hacía muy difícil verificarlo de forma manual. Pero, aun así, la respuesta ha sido dada como válida 

Estructuras de los grafos: 

Las estructuras de los grafos que se lleguen a utilizar por nosotros dependerán de los algoritmos que usemos para procesar nuestro gráfico y de las características que este mismo tenga. En la gran mayoría de las veces se usan las listas y las matrices, ya que cada una cuenta con características sencillas: Con las listas es mejor usar gráficos dispersos, ya que son eficientes en temas de capacidad a la hora de guardar nuestro gráfico en nuestra computadora; mientras con las matrices se da un acceso más rápido a nuestro gráfico, pero, a cambio, esto llega a gastar mucha memoria de nuestro computador. 

Las estructuras lisas se dividen en dos formas, las cuales son: 

1. Lista de incidencia: En este tipo de lista, las aristas son representadas por vectores pares ordenados (esto si el grafo es dirigido), donde cada par representa cada una de las aristas 

2. Lista de adyacencia: En esta lista, cada vértice tiene una lista de vértices que son adyacentes a este. En un grafo que no es dirigido, esto causará una redundancia en este, ya que, por ejemplo, un vértice X va a existir en la lista de adyacencia de Y, y viceversa (un vértice de Y estará en la lista de adyacencia de X) 

Las estructuras matricales también se dividen en dos formas, estas son: 

1. Matriz de incidencia: En esta estructura, el grafo va a estar representado por una matriz de A (que son aristas) por V (que son vértices) donde el vértice contiene información de la arista 

2. Matriz de adyacencia: Aquí la matriz es cuadrada (representada por M) con un tamaño “n” elevado al cuadrado (en este caso, n, es el número de vértices), es decir, si hay una arista entre un vértice “a” y un vértice “b”, quiere decir que el elemento “M_ab” es igual a 1, si no llega a suceder eso, es igual a 0 

Tipos de grafos:  

Hay 8 tipos existentes de grafos, los cuales son: 

1. Grafo regular: Son todos los grafos donde cada vértice tiene una equivalencia igual 

2. Grafo bipartito: Son grafos los cuales sus vértices son separados en dos conjuntos, con tal de que las aristas no se puedan relacionar vértices de un mismo conjunto, es decir, que un vértice de un el grupo A se conecte con otro vértice de un grupo B. 

3. Grafo completo: Es un grafo donde cada par de vértices está conectado con una arista 

4. Grafo nulo: Este grafo no cuenta con vértices ni con aristas. 

5. Grafos isomorfos: Usa dos grafos, los cuales son isomorfos; si existe la misma cantidad de vértices, y los vértices de cada grafo se pueden enumerar de 1 hasta un número indeterminado, con tal de que dos vértices del segundo grafo están unidos por una arista entre sí 

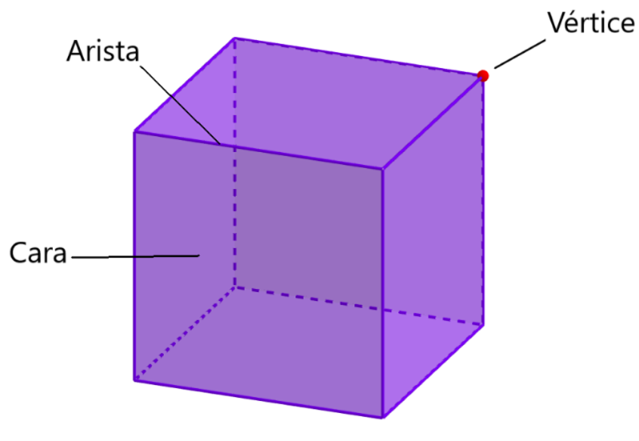
6. Grafos platónicos: Son los gráficos que tienen como base uno de los sólidos platónicos (los sólidos platónicos son: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro) y están formados por sus vértices y aristas respectivas (es decir, 8 vértices y 12 aristas del cubo)

7. Grafos conexos: Son aquellos grafos que todos sus vértices están conectados por medio de un camino o un semicamino (dependiendo si el grafo es no dirigido o dirigido). Si un grafo no está conectado por medio de un camino (o un semicamino) es considerado como un “grafo no conexo” 

8. Grafos dirigidos: También se pueden llamar “dígrafos”, estos son todos los grafos los cuales sus aristas tienen un sentido definido, es decir, cada arista tiene su destino final en el grafo  

Aplicaciones:

Esta teoría presenta múltiples aplicaciones que hacen que se pueda resolver problemas matemáticos, como en la síntesis de circuitos secuenciales, circuitos contadores o sistemas de apertura. Además, con esta teoría podemos brindar soluciones de dibujo computacional (esto relacionado con la ingeniería). 

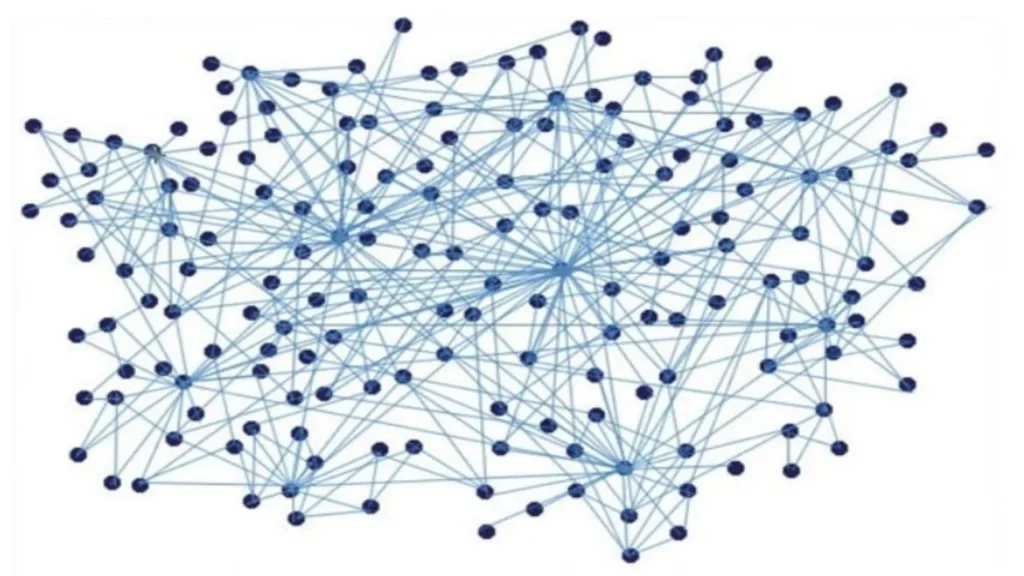
También, gracias a esta teoría, se ha podido aprovechar al máximo el uso de las redes sociales, ya que se pueden construir análisis que puedan comprender relaciones, preferencias y similitudes entre los usuarios. 

Otra de las aplicaciones de la teoría de los grafos es en el ámbito de la biología, ya que el vértice representa un hábitat y las aristas representan senderos o migraciones de los animales. Con esto, los científicos pueden entender cómo esto puede cambiar o afectar las especies en su hábitat. 

Su relación con la TGS: 

Como ya se mencionó antes, la teoría de los grafos brinda soluciones de dibujo computacional (lo cual es el uso de computadoras para crear, modificar o mejorar un diseño en específico creado por una persona). Pero no solo tiene ese uso, tiene varios usos más, algunos de estos son: 

• Contribuir a las redes sociales con funciones muy simples, por ejemplo, en Facebook en el apartado “Personas que quizás conozcas”, ya que este apartado es el resultado de un algoritmo en donde tú (que, en este caso, vendrías siendo un nodo) estás cerca de otra persona (la cual, también sería otro nodo), esto está basado en que hay una conexión con nuestros amigos directos con ese nodo, es decir, esa persona que no tienes agregada a tus amigos quizá la llegues a conocer por un amigo directo que tengas agregado en Facebook 

• Los grafos también ayudan a la construcción de mapas y esquemas, siempre buscando una ruta corta o con menos problemas en su camino (es decir, son grafos dirigidos)

• El IoT (Internet of things, en español “El Internet de las Cosas”) también está relacionado con la teoría de los grafos, un ejemplo podría ser la movilidad de las personas. Esto se fundamenta en lo siguiente: cada persona que se está moviendo en la ciudad con su celular en la mano, podría ser considerada como un nodo dentro de un grafo, esto permite detectar grandes afluencias de personas en un sector en concreto y hora del día específica dentro de la ciudad (a esto se le llama densidad). Y todo eso claramente se debe realizar con grafos. 

Otro ejemplo podría ser el siguiente: los grafos se pueden usar para representar las llamadas telefónicas hechas en una red de larga distancia. Se usa un multígrafo, dirigido para representar cada llamada. Para representar el multígrafo se toma lo siguiente: un vértice representa un número telefónico y una arista representa una llamada hecha. La arista sale del número que hace la llamada y tiene como receptor final el número al cual va dirigida la llamada   

• Se usa mucho en las bases de datos, como por ejemplo en Neo4j, esta página es una aplicación que ayuda a potencializar, descubrir y analizar relaciones en datos conectados entre sí, como, por ejemplo, poder comprender tablas de manera sencilla: los nodos del grafo representan las tablas y las aristas son las relaciones entre todas ellas. 

• Las bases de datos también pueden utilizarse como conexiones entre distintos datos, es decir, cada base de datos es un nodo, y las aristas son las conexiones que se tienen entre sí. 

• Las redes de internet pueden ser representadas mediante un grafo, el cual es dirigido, ya que cada página web está representada por un vértice y las aristas comienzan en una página A y termina en una página B, eso sí, si hay algún enlace de por medio que lleve a esa página 

Videos de apoyo:

BettaTech (26 de Agosto de 2019) GRAFOS en Ingeniería Informática | Estructuras de datos y Algoritmos. YouTube https://youtu.be/23pdz9VtIBo  

El Taller De TD (16 de julio de 2022) Teoría de GRAFOS en INFORMÁTICA: Que es un grafo, Tipos de Grafos, como representarlos y ejemplos. YouTube https://youtu.be/F5Xjpg0-NhM  

Créditos:

Autor: Gabriel Felipe Guzmán Rivera

Editor: Máster Carlos Iván Pinzón Romero

Código: UCPSG7

Universidad: Universidad Central

Fuentes:

DJ Castillo Triviño. Carlos Iván Pinzón Romero (2023). Niixer.com https://niixer.com/index.php/2023/02/28/teoria-de-las-graficas-o-grafos/
Marta Macho Stadler (2014). Cultura científica.com https://culturacientifica.com/2014/08/06/arthur-cayley-la-teoria-de-grafos-y-los-isomeros-quimicos/
Camilo Chacón Sartori (2018). Quora.com https://es.quora.com/Cu%C3%A1l-es-la-importancia-de-la-teor%C3%ADa-de-grafos-en-las-ciencias-de-la-computaci%C3%B3n
Autor Desconocido (2020). Grafos [Imagen].
https://opensistemas.com/wp-content/uploads/2020/06/Grafos.jpg  
Autor Desconocido (2023). eade1a_a796c0f2056d4a6b90a66edbb6f0048c~mv2 [Imagen]. https://static.wixstatic.com/media/eade1a_a796c0f2056d4a6b90a66edbb6f0048c~mv2.jpg/v1/fill/w_532,h_317,al_c,q_80,usm_0.66_1.00_0.01,enc_auto/eade1a_a796c0f2056d4a6b90a66edbb6f0048c~mv2.jpg 
XalD (2009). Four color world map [Imagen].
https://niixer.com/wp-content/uploads/2023/03/image-108.png 
Autor Desconocido (2021). Características de un cubo [Imagen].  https://www.neurochispas.com/wp-content/uploads/2021/03/caracteristicas-de-un-cubo.png