Teoría de Juegos

Introducción

La teoría de juegos es una disciplina que ha revolucionado la comprensión de las decisiones estratégicas en diversas áreas del conocimiento. Originada en el cruce de la matemática y la economía, la teoría de juegos ofrece un marco analítico para estudiar situaciones en las que múltiples agentes interactúan, cada uno tratando de maximizar sus beneficios en un contexto de interdependencia. Este campo no solo ha encontrado aplicaciones en la economía, sino también en la biología, las ciencias políticas, la informática, entre otros. En este artículo, exploraremos los fundamentos de la teoría de juegos, su evolución histórica, conceptos clave, y sus aplicaciones más destacadas en diferentes disciplinas.

¿Qué es la Teoría de juegos?

La teoría de juegos o teoría de las decisiones interactivas es el estudio del comportamiento estratégico cuando dos o más individuos interactúan y cada decisión individual resulta de lo que el (o ella) espera que los otros hagan. Es decir, que debemos esperar que suceda a partir de las interacciones entre individuos (Monsalve,2003)

Origen y evolución histórica de la teoría de juegos

El origen de la teoría de juegos se remonta a principios del siglo XX, aunque sus raíces conceptuales pueden rastrearse hasta tiempos antiguos. En 1928, el matemático húngaro John von Neumann publicó un artículo influyente titulado “Zur Theorie der Gesellschaftsspiele”, el cual es considerado uno de los primeros trabajos formales en la disciplina. Von Neumann introdujo el concepto de la estrategia mixta y el principio del minimax, sentando las bases para el desarrollo de la teoría de juegos como un campo de estudio (Morgenstern,1955)

Sin embargo, la teoría de juegos adquirió un estatus formal con la publicación del libro “Theory of Games and Economic Behavior” en 1944, coescrito por John von Neumann y el economista Oskar Morgenstern. Esta obra monumental no solo formalizó los principios de la teoría de juegos, sino que también los aplicó a problemas económicos, estableciendo un vínculo crucial entre la matemática y la economía. El libro presentó la idea de que las situaciones económicas podrían modelarse como juegos, donde los participantes son jugadores que toman decisiones estratégicas

John Nash:

El trabajo de von Neumann y Morgenstern sentó las bases para futuros desarrollos en la teoría de juegos. En 1950, John Nash, un joven matemático de Princeton, introdujo el concepto de “Equilibrio de Nash” en su tesis doctoral. Este concepto amplió considerablemente el alcance de la teoría de juegos, al proporcionar un marco para analizar situaciones con múltiples jugadores, cada uno con sus propias estrategias y objetivos. Nash demostró que, bajo ciertas condiciones, cada juego tiene al menos un equilibrio en el que ningún jugador tiene incentivos para desviar unilateralmente de su estrategia, lo que representa un punto de estabilidad en el juego. (Binmore,1994)

Durante las décadas de 1950 y 1960, la teoría de juegos se expandió rápidamente, atrayendo la atención de matemáticos, economistas y científicos sociales. Investigadores como Lloyd Shapley, Robert Aumann y Reinhard Selten realizaron contribuciones significativas al campo, introduciendo nuevos conceptos y aplicaciones. En 1994, John Nash, junto con Reinhard Selten y John Harsanyi, recibió el Premio Nobel de Economía en reconocimiento a sus contribuciones a la teoría de juegos, lo que consolidó la importancia de esta disciplina en el análisis económico y más allá

Conceptos clave en la teoría de juegos

Estrategias y pagos

En la teoría de juegos, una estrategia es un plan de acción que un jugador sigue en un juego. Las estrategias pueden ser puras o mixtas. Una estrategia pura es aquella en la que el jugador elige una acción específica con certeza, mientras que una estrategia mixta implica la selección de acciones basadas en una distribución de probabilidad. El concepto de estrategias mixtas es particularmente relevante en situaciones donde no existe una estrategia pura dominante, y se ha explorado ampliamente en estudios teóricos y empíricos

El concepto de pago o payoff se refiere a la recompensa que un jugador recibe como resultado de sus acciones dentro del juego. Los pagos pueden ser cuantificables, como ganancias monetarias, o cualitativos, como la satisfacción de ciertos objetivos. La teoría de juegos se centra en cómo los jugadores eligen sus estrategias para maximizar sus pagos, considerando las posibles acciones de los demás jugadores. Este enfoque es crucial en la modelización de mercados y en la teoría económica en general

Equilibrio de Nash en la teoría de Juegos

El Equilibrio de Nash es uno de los conceptos más fundamentales en la teoría de juegos. Se refiere a una situación en la que ningún jugador puede mejorar su situación cambiando su estrategia de forma unilateral, dado que los demás jugadores mantienen sus estrategias sin cambios. Este equilibrio representa un punto de estabilidad dentro del juego y ha sido un pilar en el análisis de interacciones estratégicas en economía, política y otras áreas (Gibbons,1992)

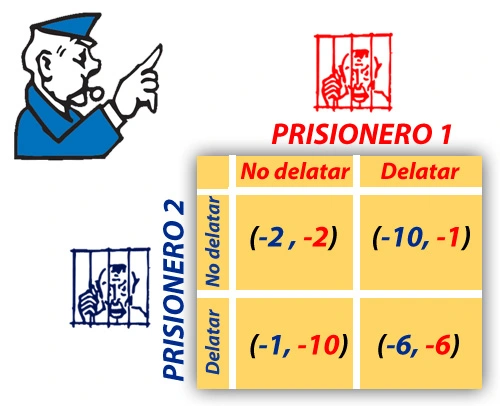
El dilema del prisionero

Es uno de los dilemas mas famosos en juegos. En este se presentan a dos fugitivos, vamos a llamarlos Carlos y Ángel. El fiscal del distrito sabe que son culpables de un crimen importante pero no podrá aprenderlos si uno de los dos no confiesa, así que se le ocurre ordenar su detención para ponerlos en cuartos diferentes, donde les ofrece el siguiente acuerdo:

• Si confiesas y tu cómplice no confiesa, sales en libertad.
• Si tu no confiesas, pero tu cómplice confiesa, te sentenciaran con la condena mas larga en la cárcel.
• Si los dos confesáis, ambos seréis encarcelados, pero no se aplicará la condena más larga.
• Si ninguno de los dos confiesa, ambos seréis incriminados con cargos de evasión fiscal con los que la pena de prisión está asegurada (Binmore,1994)

Tipos de juegos

La teoría de juegos clasifica los juegos en varias categorías según diferentes criterios. Dos de las distinciones más comunes son entre juegos cooperativos y no cooperativos, y entre juegos de suma cero y de suma no cero.

• Juegos cooperativos: En estos juegos, los jugadores pueden formar coaliciones y hacer acuerdos vinculantes para mejorar sus pagos conjuntos. Este tipo de juegos es relevante en situaciones donde la cooperación puede llevar a resultados más beneficiosos para todos los participantes, como en la formación de alianzas políticas o empresariales

• Juegos no cooperativos: Aquí, los jugadores toman decisiones individualmente, y no se permite la formación de coaliciones vinculantes. La mayoría de los análisis en teoría de juegos se centra en este tipo de juegos, en los que los jugadores actúan de manera estratégica e independiente, como en la competencia entre empresas en un mercado

• Juegos de suma cero: En estos juegos, la ganancia de un jugador es exactamente la pérdida de otro, lo que significa que la suma de los pagos es cero. Un ejemplo clásico es el ajedrez, donde un jugador solo puede ganar si el otro pierde. Estos juegos son fundamentales en el estudio de conflictos y guerras, donde los intereses de las partes son completamente opuestos

• Juegos de suma no cero: Estos juegos permiten la posibilidad de que todos los jugadores se beneficien o sufran pérdidas, lo que crea oportunidades para la cooperación y el beneficio mutuo. Un ejemplo podría ser la negociación internacional, donde ambas partes pueden llegar a un acuerdo que mejore su situación respecto al punto de partida

   Aplicaciones de la teoría de juegos en diferentes campos

Economía

Una de las áreas donde la teoría de juegos ha tenido un impacto significativo es en la economía, particularmente en la teoría de mercados y la organización industrial. La teoría de juegos se utiliza para modelar y analizar cómo las empresas competidoras interactúan en un mercado, previendo cómo la competencia y la cooperación entre empresas afectan los precios, la producción y el bienestar general. Los modelos de oligopolio, como el modelo de Cournot y el modelo de Bertrand, son ejemplos clásicos donde la teoría de juegos se aplica para entender cómo las empresas deciden sus niveles de producción y precios, considerando las acciones de sus competidores.

Además, la teoría de juegos se utiliza para analizar subastas y mercados de licitaciones, donde múltiples agentes compiten por bienes o contratos. Las subastas, como la subasta de Vickers o la subasta inglesa, pueden ser modeladas utilizando la teoría de juegos para entender las estrategias óptimas de los participantes y el diseño eficiente del mecanismo de subasta. Estas aplicaciones son fundamentales en mercados como el de telecomunicaciones y energía, donde las licitaciones competitivas son comunes.

Ciencias políticas

En ciencias políticas, la teoría de juegos se aplica para analizar el comportamiento estratégico en elecciones, formación de coaliciones, y negociaciones internacionales. Uno de los modelos más influyentes es el modelo espacial de competencia política, que utiliza la teoría de juegos para predecir cómo los partidos políticos posicionan sus plataformas políticas en un espectro ideológico para maximizar los votos. Este modelo ha sido utilizado para entender la dinámica de las elecciones en democracias multipartidistas y cómo los partidos deciden sus posiciones estratégicas.

Otro campo de aplicación es la formación de coaliciones. La teoría de juegos cooperativos proporciona herramientas para analizar cómo los partidos o países pueden formar coaliciones para alcanzar objetivos comunes.

Biología

La teoría de juegos ha sido ampliamente adoptada en biología, particularmente en el estudio de la evolución y el comportamiento animal. La teoría de juegos evolutiva, una rama de la teoría de juegos se utiliza para modelar cómo las estrategias de comportamiento se propagan en una población a lo largo del tiempo

Video de Apoyo

Créditos:

Autor: Juan Esteban Quintero Tapia

Editor: Carlos Iván Pinzón Romero

Código: UCPSG4-1

Fuentes:

Fuentes Articulo:

Morgenstern, O. (1955). La teoría de los juegos y del comportamiento económico. Económica, 1.

Binmore, K. (1994). Teoría de juegos. Madrid: McGraw-Hill.

Gibbons, R. (2022). Un primer curso de teoría de juegos. Antoni Bosch Editor.

Franco, J. C. A. (2006). Teoria de la Decision y de los Juegos. Delta publicaciones.

Elster, J. (2015). Marxismo, funcionalismo y teoría de juegos: Alegato en favor del individualismo metodológico. Sociológica México, (2).

imagenes

CeCo (2023). iStock [ imagen]. Centro Competencia. https://centrocompetencia.com/wp-content/uploads/2023/03/iStock-1202205418-1024x540.jpg

FECYT (2011). dilema_del_prisionero_teoria_juegos [imagen]. Observatorio de la ciencia cuidadana en España. https://ciencia-ciudadana.es/wp-content/uploads/2021/02/dilema_del_prisionero_teoria_juegos-402x327.jpg

BrainPop (s.f). screenshot1 [imagen]. BrainPop Maestros. https://cdn.brainpop.com/mx/salud/psicologia_y_comportamiento/teoria_de_juegos/screenshot1.png

23.claudiatoledo(s.f). TeporiaJuegos [imagen]. Emaze.https://userscontent2.emaze.com/images/7af9d11a-6b43-48a6-b535-9a9473be765d/8b149f8baa2727038c931aaa8df86d6d.jpg


Video

SCP EXPLICADO. (18 de diciembre 2019). ¿Que exactamente es la teoria de juegos?[Video]. Youtube. https://youtu.be/KtQVHasZRbA?si=4vvEo9VVorljpDhm