Teoría de las catástrofes

slideplayer.es/amp/3828138/(abre en una nueva pestaña)
Se conoce la teoría de las catástrofes de René Thom como un gran avance en las matemáticas modernas.
Para facilitar su comprensión se resaltan algunos autores y las principales ideas o conjeturas que significaron un gran aporte en la formulación y consolidación de esta nueva forma de concebir los sistemas dinámicos.
Recuento de las mentes brillantes que aportaron a concretar la teoría de las catástrofes
Desde la antigüedad el ser humano ha intentado descubrir y comprender las dinámicas que rigen nuestro universo, posiblemente el inicio fue marcado por explicar nuestra realidad con creencias religiosas que establecen un orden a partir de la creación.
Con el pasar del tiempo, el desarrollo del pensamiento y con él, la consideración de la razón se formularían nuevas formas de percibir el orden de los sistemas.
En la Antigüedad se gestaron las primeras bases matemáticas en las que se contemplaron el caos como parte esencial del orden de las cosas, pero tuvieron que pasar siglos para que se volvieran a retomar éstos pensamientos como parte de las matemáticas.
Examinando a Aristotéles en la Antigua Grecia encontramos que cuando declaró “Si la totalidad del cuerpo está ahora en este orden y más tarde en otra, y si forma parte de una totalidad, entonces no será el mundo el que se genere y se destruya, sino solamente la disposición de sus partes” se estaba acercando a la noción de que el desorden es parte de cualquier sistema y que inevitablemente regresará a un nuevo orden.
En este orden de ideas también consideraremos a Platón, quien concebía la complejidad del “mundo como un todo, con un orden, organización y estructura donde todas las partes se hallan en armonía con las demás”.
Épocas más tarde encontramos a René Descartes quién promueve un enfoque reduccionista para el estudio de la complejidad cuyo principal principio está basado en “El todo es igual a la suma de las partes”.
Los primeros indicios
Continuamos con Henry Poncaire “Pequeñas diferencias en las condiciones iniciales engendran otras muy grandes en las situaciones resultantes, y el mínimo error en identificar las primeras ocasionaría un enorme error en identificar las últimas”.
Es así como podemos observar la aparición de los primeros indicios de una nueva forma de concebir la realidad en la que estamos inmersos.
A lo largo de la comprensión de este nuevo concepto se encuentran autores importantes que contribuyeron en la consolidación del mismo. George Cantor con la teoría de conjuntos, George Boole, el teorema de Gödel sobre la incompletitud de la deducción matemática, el principio holístico de Smuts.
Von Newman con la teoría de autómatas en la que se toma como objeto de estudio no a los elementos en sí, si no a su conducta y cómo esta determina en gran medida un resultado o estabilidad.
Teoría de las catástrofes
Finalmente en los años 90 aparece la teoría de las catástrofes de René Thom, que pretende una comprensión del desorden en la discontinuidad. La divergencia empieza a crecer hasta tener resultados incomprensibles.
En general habla de alteraciones en sistemas dinámicos, sucesos que pueden ocurrir en todos los ámbitos; especialmente en aquellos en los que tanto el número como la naturaleza de variables que interfieren no permiten un cálculo en el intento por predecir un resultado.
Aplicaciones de la teoría de las catástrofes
El desarrollo tecnológico de las últimas décadas ha permitido evidenciar su practicidad en ámbitos biológicos, geológicos, económicos, psicológico y sociales. Un ejemplo sencillo puede ser cómo el cambio de tono de una persona en medio de una conversación puede alterar a los demás participantes de la misma y terminar en una terrible riña.
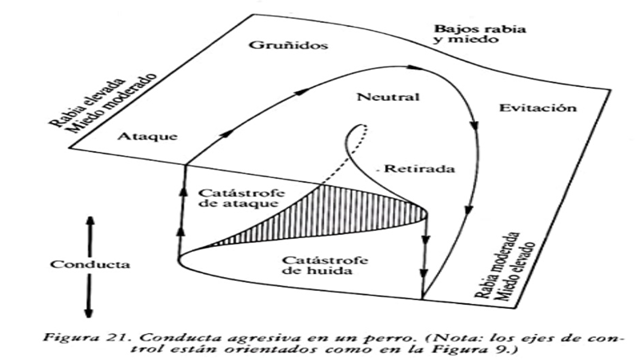
El ejemplo más conocido es el del perro que de acuerdo a sus impulsos terminará atacando y el cambio en su conducta terminará desencadenando una “catástofre”.
Durante el siglo pasado es donde más se ha podido ver la practicidad de la teoría aplicada, más concretamente con la invención de los ordenadores y programas de software (Windows) y es que son innumerables las disciplinas en donde encontrar aplicaciones prácticas.
- Ingeniería de Sistemas
- Gestión de Sistemas
- Investigaciones Operativas
- Sistemas en función de modelos de problemas por resolver.
Características en común
En general estos sistemas presentan las siguientes características:
- Estudio de los componentes y sus relaciones como parte de la estructura de un sistema
- Estudio del sistema sin aislarlo del entorno
- Uso de un ordenador en vez de las ecuaciones matemáticas para establecer patrones que permitan la simulación de diferentes alternativas.
Ahora, es evidente que la teoría que le otorgó al matemático francés gran reconocimiento se evidencia en la naturaleza de todos los sistemas. Puede dar cuenta o respuesta a múltiples preguntas que reconocidos personajes de la ciencia han querido dilucidar.
Es que es innegable que aquello que no parece enmarcarse en un orden específico pueda ser parte de todos los sistemas conocidos. Es inevitable que irrumpan en el equilibrio de ellos, es decir está tan presente en nuestra realidad como aquellos fenómenos de un sistema determinista.
Estudios posteriores dan cuenta de lo importante y práctico que es el nuevo enfoque en el estudio de sistemas dinámicos, con lo que se alcanzaría nuevos conceptos y teorías como la teoría del caos, teoría de las bifurcaciones, teoría de Fractales, teoría de las estructuras disipativas.
Conclusiones
El abordar la naturaleza del todo genera la comprensión de diversos fenómenos y posibilita la previsión de los mismos. Es por eso que esta nueva forma de concebir “el desorden” nos acerca más a trabajar con situaciones de nuestra cotidianidad.
Comprender que aislar los sucesos ha facilitado en gran manera el desarrollo científico y tecnológico de nuestra sociedad. Sin duda, una mirada más amplia de la naturaleza de los sucesos nos permitirá avances en sistemas más complejos. Comprender el todo como algo diferente a la suma de sus partes sin duda abre campos de investigación enormes.
Autor: Yesica Viviana Micanquer Quenan
Editor: Carlos Iván Pinzón Romero
Código: UCPS-1
Universidad: Universidad Central
Fuentes
García, J.M. () .Teoría de las catástrofes. ATC- INNOVA. http://www.dinamica-de-sistemas.com/cursos/sysware0.htm
http://www.dinamica-de-sistemas.com/cursos/sysware0.htm
http://goodreads.com/review/show/3645692216
https://slideplayer.es/amp/3828138/
https://slideplayer.es/amp/3828138/
https://www.timetoast.com/timelines/historia-de-las-matematicas-aeba0ad5-bc26-4a0e-8c9a-5c21b76ea4a6