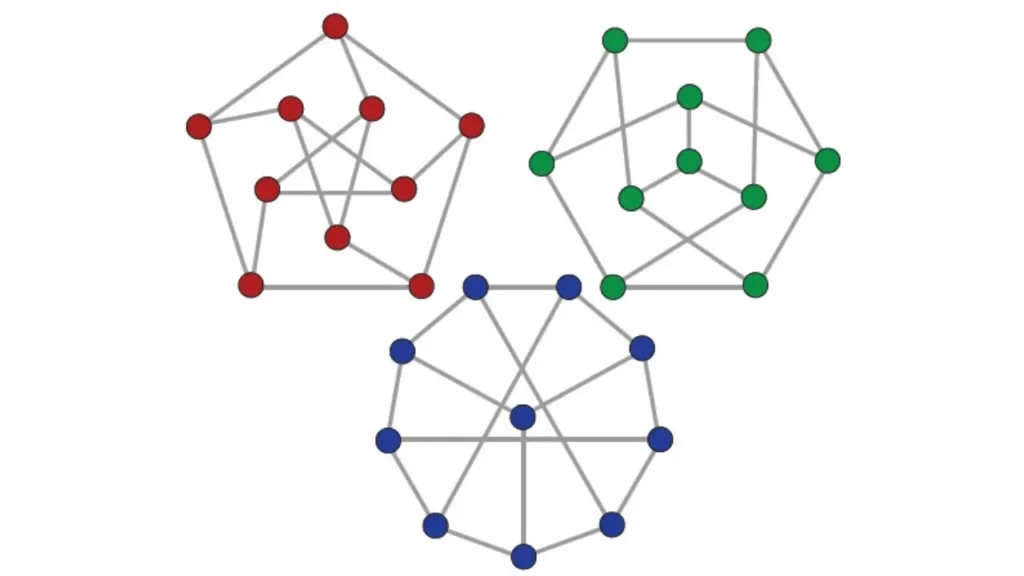
Teoría de las gráficas
¿Qué es la teoría de las gráficas?, es una rama de las matemáticas discretas que ha ido teniendo un gran avance en los últimos años gracias a que es una herramienta muy útil y eficaz, logrando así ser utilizada en otras áreas como la química, ciencias sociales, lingüística, física y otras; jugando además un papel muy importante en el área de la ciencia de la computación. En nuestra vida cotidiana también utilizamos inconscientemente esta teoría, algunos ejemplos claros los podríamos identificar en el modelado de redes sociales, de transporte, eléctricas, moleculares, etc.
En este articulo tendré como propósito dar a conocer la teoría de las gráficas, basándome en los conceptos clave y tomando teoremas fundamentales para entender y aplicar esta teoría.
CONCEPTOS CLAVE Y RESULTADOS INICIALES
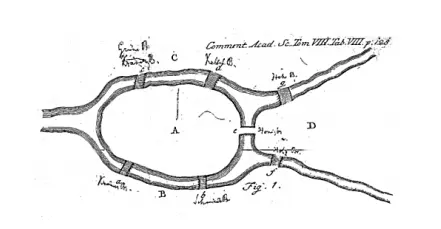
El problema de los Puentes de Königsberg: surgió en la actual cuidad de Kaliningrado en el siglo XVIII, que tenía dos islas conectadas a la orilla por siete puentes. La pregunta era si se podía caminar por la ciudad pasando por cada puente una vez y regresar al principio. En 1739 Leonhard Euler resolvió el problema dibujando la situación con una gráfica, los lugares representando vértices y los puentes representando aristas. Euler demostró que en vista de que la gráfica tenía vértices con grados impares, un trayecto que pasara por cada puente una vez y regresara al principio no era posible.
El resultado de Euler propuso conceptos fundamentales en la teoría de las gráficas, como la importancia de los grados de los vértices en los recorridos y sentó bases para el desarrollo de las matemáticas.
GRÁFICAS :
Es una estructura matemática que representa las conexiones y relaciones entre objetos. Dos ordenadas G=(V,E), que crea una gráfica, donde:
-Se le llama V a un conjunto de vértices (o nodos), que representan los objetos o entidades.
-Se le denomina E es un conjunto de aristas (o enlaces), que representan las conexiones o relaciones entre los vértices.
–Subgráfiacas: si el conjunto de los vértices de G es un subconjunto de los vértices de G y el conjunto de las aristas de G es subconjunto de las aristas de G, una gráfica G’ seria una subgrafica de G.
-Isomorfismos: es una conexión que define una igualdad estructural entre dos gráficas. Si dos gráficos tienen la misma estructura, es decir, si se pueden asimilar iguales desde el punto de vista donde se conectan, se consideran isomorfos, sin embargo, los nombres de los vértices y etiquetas de las aristas pueden variar. Permite reconocer y ordenar las gráficas con la misma estructura subyacente.
-Conexas: la familia de las gráficas conexas es una de las más importantes en este concepto. Decimos que, si existe una trayectoria uv en G, dos nodos u y v de una gráfica G están conectados. Si para todo par de vértices o nodos u y v de la gráfica G existe una trayectoria uv, es decir, si u y v estan conectados la gráfica va a ser conexa. Si H no aparece en ninguna subgráfica conexa de G con más vértices o más aristas que H, diremos que H es una componente conexa de G.
-Bipartitas: si se encuentran dos conjuntos A y B de los vértices de una gráfica G de manera que:
A ∪B = V (G). Si uv pertenece a E(G), U pertenece a A y V a B.
DIGRÁFICAS:
Si consideramos flechas en vez de aristas, Una digráfica se puede entender a partir de una gráfica. En otras palabras, una digrafica D es una estructura formada por V (D) un conjunto de vértices y F(D) un conjunto de parees ordenaos de V(D) conocidos como flechas o arcos. Hay que tener en cuenta que cunado consideramos pares ordenados, asignamos una dirección a la flecha. Si queda claro que estamos hablando de las flechas de una digrafica, indicaremos como uv para un par ordenado (u, v) en F(D).
ÁRBOLES Y SUS APLICACIONES EN GRÁFICAS
Un árbol es una gráfica conexa sin ciclos.
Se presentaron por Arthur Cayley para contar estructuras químicas y se consideraron estructuras matemáticas en la teoría de las gráficas. Las leyes Kirchhoff fueron creadas por Gustav Kirchhoff y se aplicaron a las redes eléctricas, la química molecular y las ciencias de la computación, depende principalmente para diseñar algoritmos y estructuras de datos.
Mientras que los árboles se pueden expresar con arreglos y matrices, la ilustración dinámica con almacenaje unido es más común en computación porque es más fácil insertar y eliminar vértices.
Por su facilidad de uso, se enfoca en los árboles binarios. Cualquier árbol general puede transformarse en un árbol binario equivalente. Además, la eliminación de vértices o aristas tiene un impacto en la unión de una gráfica, con ejemplos de gráficas cuya conexidad no cambia al eliminar ciertos
RECORRIDOS EN GRÁFICAS
Muchos problemas de este tipo pueden mostrarse a través de gráficas, y las soluciones a estos problemas dan lugar a dos familias importantes de gráficas: las gráficas Eulerianas y Hamiltonianas.
Gráficas Eulerianas:
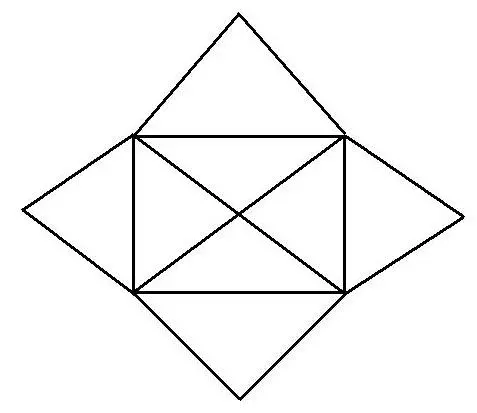
Es una gráfica que le permite recorrer todas sus aristas solamente una vez. La idea proviene del problema de los Puentes de Königsberg que mencione anteriormente, el juego de dibujar la firma del diablo que representa los conceptos de los caminos y ciclos eulerianos. Es una forma de entrar a la familia de las gráficas eulerianas. Consiste en dibujar una figura compleja sin levantar el lápiz ni trazar una línea dos veces, el recorrido es posible Si la gráfica asociada cumple con las condiciones mencionadas.
Gráficas hamiltonianas:
Son aquellas que tienen un ciclo que visita cada vértice una vez y luego regresa al punto de partida. El Juego Icosian que se juega sobre un dodecaedro regular, con cada vértice representando una ciudad europea dio lugar a la idea. El objetivo es descubrir un camino que recorra todas las ciudades (vértices) una vez y regrese al punto de inicio. Este problema demuestra la necesidad de encontrar un ciclo hamiltoniano en la gráfica que corresponde al dodecaedro.
PLANARIDAD Y CONEXIDAD
Planaridad:
El termino se refiere a la capacidad de una gráfica para dibujar en un plano sin puntos de encuentros de aristas. Los grafos planos son importantes para el diseño de redes y circuitos físicos. Para determinar si una gráfica es plana es bueno tener en cuenta las siguientes observaciones:
1. Toda subgráfica de G es plana si G es una gráfica plana.
2. Si la subgráfica de G no es plana. Como resultado, G no es plana.
Conexidad:
Indica si una gráfica está completamente interconectada, lo que significa que hay caminos entre los pares de vértices. Es importante en redes de comunicación y transporte para asegurar la redundancia y la accesibilidad.
En la teoría de las gráficas ambos conceptos son fundamentales para poder resolver problemas y tienen aplicaciones prácticas en campos como en áreas que van desde el diseño de redes hasta y la planificación de circuitos.
COLORACIONES DE GRÁFICAS
El problema de coloración en teoría de las graficas, se centra en asignar colores a los vértices o aristas de una gráfica para cumplir ciertas condiciones.
Hace más de cien años se debatió el problema de los cuatro colores. En 1852 Augustus de Morgan le preguntó a Sir William Hamilton por qué un mapa puede ser coloreado con cuatro colores para que dos regiones cercanas no compartan el mismo color. Al convertir el mapa en una gráfica plana, donde cada región es un vértice y cada frontera compartida es una arista la teoría de las gráficas nos ayuda a entender este problema. Actualmente se cree que cualquier gráfica plana puede ser coloreada con cuatro colores de manera que ningún vértice cercano comparta el mismo color.
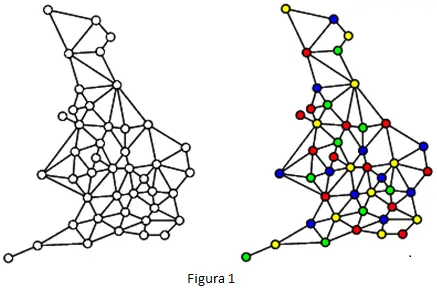
Coloración de vértices:
Se trata de asignar colores a los vértices de una gráfica para que los vértices que están cerca tengan colores diferentes. El número mínimo de colores necesarios para lograr esto es uno colorido. La teoría incluye teoremas importantes, como el de los cuatro colores y una variedad de algoritmos para encontrar coloraciones efectivas. En varios campos, como la programación de horarios, la elección de frecuencias y el diseño de circuitos están técnicas son útiles.
Algoritmo Greedy:
El algoritmo Greedy es un método para encontrar aproximadamente la coloración de los vértices. Funciona seleccionando colores a cada vértice de la gráfica uno por uno, eligiendo el primer color disponible para que no cause conflicto con los vértices que ya han sido coloreados.
Sudoku:
El Sudoku es un juego en el que los jugadores deben llenar las casillas de una cuadricula de 9 por 9 que se divide en cuadriculas o conocidas también como cajas de 3 por 3. para lograrlo, se deben cumplir las siguientes reglas:
1. los números deben ir del 1 al 9 para llenar cada casilla.
2. el mismo número no puede aparecer dos veces en el mismo renglón.
3. el mismo número no puede repetirse en la misma columna.
4. el mismo número no puede volver a colocarse en una caja de 3 por 3.
Coloración por Aristas:
Si se asignan colores a las aristas de la gráfica de manera que dos aristas aledañas (que comparten un vértice) no tengan el mismo color.
Diremos que la gráfica G= (V, E) tienen una coloración por aristas.
Video referencia:
Créditos:
Autor: Laura Julieth Moreno Triana
Editor: Carlos Iván Pinzón Romero
Código: UCPSG5-2
Universidad: Universidad Central
Fuentes:
Araujo Pardo, G & Valencia Saravia, P. (2003). Un vistazo a la teoría de gráficas. Revista ciencias unam. https://www.revistacienciasunam.com/en/busqueda/autor/86-revistas/revista-ciencias-67/747-un-vistazo-a-la-teoria-de-graficas.html
Armenta Castro, M. (1996). "CARACTERIZACIONES FUNDAMENTALES EN TEORIA DE GRAFICAS: TEORIA DE MENGERR, BROOKS, EULER, DIRAC, BERGE”. Lic mat uson max. https://lic.mat.uson.mx/tesis/90TesisMaricela.PDF
Arnold Reiners , W, Dean Prager, S. (2009). Un grabado del artículo de Euler sobre los puentes de Königsberg. [imagen]. ResearchGate. https://www.researchgate.net/profile/William-Reiners/publication/267284666/figure/fig4/AS:668770695647261@1536458767780/An-engraving-from-Eulers-paper-on-the-bridges-of-Koe-nigsberg-Alexanderson-2006.png
Badillo, E. (2002). TEORIA DE GRAFICAS. Computación tripod. http://ebadillo_computacion.tripod.com/teoria_de_graficas.pdf
El Taller De TD. (16 julio 2022). Teoría de GRAFOS en INFORMÁTICA: Que es un grafo, Tipos de Grafos, como representarlos y ejemplos. . YouTube. https://www.youtube.com/watch?v=F5Xjpg0-NhM&t=30s
Gonzales Moreno, D. (2017). Introducción a la teoría de las gráficas. ILITIA - Repositorio Institucional de la UA. http://ilitia.cua.uam.mx:8080/jspui/handle/123456789/993
Reyes Figueroa, A. (2016). Clasificación de los idiomas mediante coloración de Grafos. [imagen]. Ecfm usac. https://ecfm.usac.edu.gt/sites/default/files/2016-07/Cromatico_1.PNG
Rodríguez, L. (2019). Teoría de grafos. [Imagen]. WordPress. https://lizardorodriguez.wordpress.com/unidad-3/teoria-de-grafos/
Sánchez, K. (2015). La firma del diablo. [imagen]. Blogspot. http://1.bp.blogspot.com/-cxO2RbccKt8/Vi_ohUZxoEI/AAAAAAAAASs/deA256TgYCw/s1600/FirmaCachudo.JPG








