¿Qué es la dimensión fractal?
La dimensión fractal es un espacio, el cual si se compara a la dimensión topológica y resulta ser mayor, el sólido o patrón se define como un fractal.
La dimensión fractal puede abstraerse de varias formas, dos de las más simples e importantes para entenderla son la dimensión de autosemejanza o autosimilaridad y el recuento o conteo de cajas; consisten en determinar el valor de la dimensión del fractal sin proporcionar un papel relevante a la escala, esto brinda mayor independencia a la hora de realizar los cálculos de la dimensión.
Dimensión de autosemejanza o autosimilaridad
Esta dimensión define a los fractales como una composición de copias exactas de sí mismos cada vez a una menor escala, dos ejemplos clásicos son la Curva o copo de Von Koch y el Triángulo de Sierpinski.
| Curva o copo de Von Koch | Triángulo de Sierpinski |
Cálculo:
Variable
| Nombre | Representación |
| Escala | ε |
| Repeticiones | N |
| dimensión | d |
Siguiendo la definición de la geometría convencional que define la dimensión de los objetos geométricos como
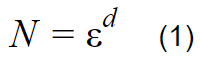
Realizando un despeje de la ecuación (1)

Con la ecuación (2) se puede calcular la dimensión de un fractal autosemejante o automilar.
Recuento o conteo de cajas
En caso de que el objeto geométrico o fractal del que se quiere hallar la dimensión no sea autosimilar o autosemejante, se realiza una visión más general en el espacio. Se realiza una abstracción de una figura geométrica con una dimensión topológica conocida como la línea, el cuadrado o el cubo cuyas dimensiones son 1, 2 y 3 respectivamente, el criterio para seleccionar la figura es la que más se asemeje al fractal; luego se superpone la figura y se cuenta las unidades repetidas sobre los objetos geométricos que pasen por la línea.
El recuento de cajas es un ejemplo de colocar una regla y revisar cuántos objetos se repiten.
Un ejemplo de un fractal que no es autosimilar o autosemejante, es el conjunto de Cantor.
Cálculo:
Variable
| Nombre | Representación |
| Longitud | L |
| Número de segmentos | N(ε) |
| Longitud de segmento | ε |
| Área geométrica |
La representación gráfica para el cálculo de la dimensión fractal por conteo de cajas es:
Para medir la longitud L se deben contar el número de segmentos N(ε), los cuales poseen una longitud ε. El número de repeticiones es representado en la siguiente ecuación

Nota: El exponente representa la dimensión topológica de la línea.
Para medir el área de una superficie bidimensional, se realiza la representación anterior en los ejes x y y del plano cartesiano
En general, para un espacio de dimensión d, se dice que
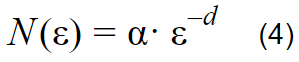
Con este análisi se realiza el despeje a la ecuación (4)
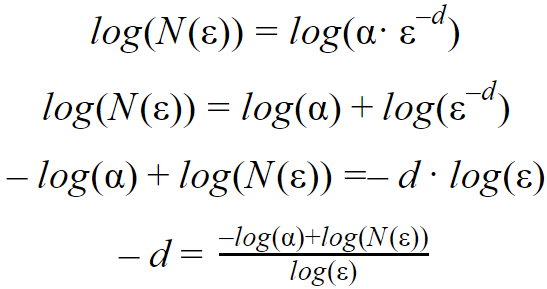
Como un fractal no posee un área definida, se realiza una aproximación realizando el límite de tendiendo a cero (para hacer que el área sea lo más mínima posible).

Con la ecuación (5) se puede calcular la dimensión de cualquier fractal, pero en caso de que el fractal sea auto semejante es recomendable usar la ecuación (2), ya que en cierto punto se vuelve complejo definir cuántos segmentos son los que colindan con la figura seleccionada, ya que son simétricos y por lo tanto pueden existir secciones en blanco o “vacías”.
Autor: Julián Andrés Guerrero Topa
Editor: Carlos Pinzón
Código: UCCG-8
Universidad: Universidad Central
Fuentes
UPM (Universidad Politécnica de Madrid). (07 de Mayo de 2018). MOOC Caos 5.2: Dimensión fractal. [Video]. Youtube. https://www.youtube.com/watch?v=-36sHrtrqKw
José Ignacio Argote. (06 de abril de 2013). Dimensión fractal. [Página web]. Mundo fractal. http://www.asociacionceat.org/aw/2/dimension_fractal.htm
José Ignacio Argote. (06 de abril de 2013). Objetos fractales. [Página web]. Mundo fractal. http://www.asociacionceat.org/aw/2/objetos_fractales.htm
Anónimo. (29 de septiembre de 2018). El conjunto de Cantor. [blog web]. matemelga. https://matemelga.wordpress.com/2018/09/29/el-conjunto-de-cantor/
Barbara A Lane. https://pixabay.com/es/users/barbaraalane-756613/

