La Teoría De Las Catástrofes

¿Qué sabemos De Catástrofes?
Conocemos una catástrofe como; un evento trágico que produce una gran destrucción o daño también podemos decir que, es un cambio brusco de estado de un sistema dinámico, provocado por la más mínima alteración de uno de sus parámetros, entonces como primer tema abordamos con exactitud una teoría que fue diseñada en base a las matemáticas y los cálculos diferenciales para dar algún tipo de explicación matemática y concisa.
¿Qué Es Un Sistema Dinámico?
Un sistema dinámico es un sistema cuyo estado evoluciona con el tiempo. Los sistemas físicos en situación no estacionaria son ejemplos de sistemas dinámicos, pero también existen modelos económicos, matemáticos y de otros tipos que son sistemas abstractos y a su vez son sistemas dinámicos es decir son los que estan es constante cambio.
¿Qué Es La Teoría De Las Catástrofes?
Esta es una Rama de los estudios de las bifurcaciones de sistemas dinámicos, esta resulta útil para el estudio de los sistemas dinámicos, que representan fenómenos naturales y que por sus magnitudes y características no pueden ser descritos de manera exacta por el cálculo diferencial, asi que es un modelo matemático de morfogénesis, cabe resaltar que la teoría de Thom se centra en el punto critico en donde aparece la bifurcación de un sistema en forma de discontinuidad, las catástrofes son definidas por los cambios bruscos y discontinuos producidos por la variación continua de fuerzas dentro de un sistema.
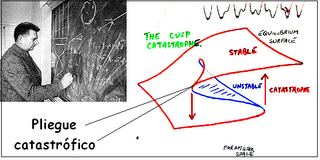
Dentro de las siete catástrofes que ideo Rene Thom tenemos las que son El pliegue o flexión que sirve para un parámetro de entrada y uno de salida tendría una formula asi: 
Inicialmente tenemos la Fruncido o cúspide que la utilizamos para dos parámetros y su fórmula seria asi: 
Asi como también tenemos La Cola de Milano donde tendríamos la formula: 
Y vendría también tenemos El ombligo Hiperbólico que sería la onda o portafolios y su fórmula se representaría asi: 
También tenemos El ombligo Elíptico o el pelo o pirámide y su fórmula estaría representada de la siguiente forma: 
Como tal también tendríamos la Mariposa y su fórmula estaría representada de la siguiente forma:
También tenemos el Ombligo Parabólico o el hongo donde su fórmula estaría definida de la siguiente manera:
Cabe Resaltar que Rene Thom mismo le asigno estas formulas a cada catástrofe.
La conclusión mas conocida obtenida por Thom es que existes 7 formas posibles de catástrofes para todas las ecuaciones que tengan más de cuatro parámetros. Cada una recibe el nombre en relación con su forma “elemental”.
¿Quién Ideo Esta Teoría?
Esta Teoría fue creada principalmente por el matemático Rene Thom para explicar tanto fenómenos topológicos y discontinuos con la ayuda de modelos matemáticos continuos, esta es una teoría de la acción, pues los modelos propuestos estudian la reacción de un sistema a la acción constituida por un estímulo. Esta basado en una serie de teoremas de la geometría de un numero de dimensiones.
¿Quién fue Rene Thom?

El matemático Rene Thom nacido en septiembre de 1923 en Montbéliard, Francia formado en el Lycée Saint-Louis y la escuela normal superior fue profesor en Grenoble y Estrasburgo.
Aunque conocido por su desarrollo de la teoría de las catástrofes entre 1968 y 1972, su primer trabajo tuvo que ver con la topología y en especial con la rama llamada topología diferencial. En topología produjo un concepto que por su importancia es hoy de frecuente uso, el cobordismo, al cual ha definido de este modo dos variedades compactas de dimensión n son cobordantes si su reunion constituye el borde de ora variedad compacta de dimensión n+1.
Sabemos que Thom es autor de varias obras científicas como la “Théorie des catastrophes et biologie” (1979), “Paraboles et catastrophes” (1983) y “Prédire n’est pas expliquer” (1991), entre otras más.
¿Cómo Thom llega a formular esta teoría?
Esta Teoría tiene su origen en el trabajo de Thom donde sus investigaciones surgen por su interés, la casualidad y el determinismo que despertó bien temprano en el Thom filósofo y su preocupación por estos problemas llegaron a la cúspide de su pensamiento en el momento de su controversia con los secretarios del caos.
Thom empieza estudiando el tema de la continuidad y discontinuidad topológica donde descubrió que el matemático Stephen Smale en la década de los 60’s comprendió que la topología se podía usar para visualizar sistemas dinámicos, y se sirvió de una clase de pliegue topológico.
Thom uso esta teoría para describir el cambio de la estructura de un sistema a lo largo de un paisaje morfológico continuo que incluye saltos ocasionales. Con ello intenta explicar como formas discretas pueden emerger de la homogeneidad y hacer crecer efectos discontinuos en la continuidad.

Características De La Teoría De Las Catástrofes
Dentro de las características encontramos 3 principales que serían la Discontinuidad, la Divergencia y la Histeria.
La discontinuidad implica que se pueden presentar cambios repentinos del comportamiento y de los resultados, asi al llegar a cierto punto no es posible manteniéndose en el mismo estado y se sufre un brusco cambio, es decir, son parámetros que de ninguna forma no tienes previsto, pero suceden.
La divergencia es la tendencia de las pequeñas divergencias para crear grandes divergencias, por ejemplo, puede que sea una compañera aérea que tiene la obligación de satisfacer toda la demanda de pasajeros si el avión habitual tiene una capacidad de 100 pasajeros, osea una demanda de 101 motivara la necesidad de utilizar un avión mayor o incluso un aterrizaje en un aeropuerto distinto. En pocas palabras las variaciones pequeñas del punto inicial de partida derivan a un resultado totalmente alejado.
La Histeria es el estado que depende de la historia previa, pero si los comportamientos se invierten conducen a que nos devuelva a la situación inicial.
Esta teoría tiene aplicaciones en muchos campos, desde la física y la biología hasta la economía y la psicología. Se ha utilizado para comprender fenómenos como, la divergencia de sistemas dinámicos, el equilibrio de ecosistemas, la formación de patrones naturales y la selección en condiciones inciertas.
Créditos:
Autor: David Alejandro Torregrosa Saad
Editor: Carlos Iván Pinzón Romero
Código: UCPSG7-1
Universidad: Universidad Central
Wikipedia.org. (2024) Teoría de las catástrofes. Wikipedia. https://es.wikipedia.org/wiki/Teor%C3%ADa_de_las_cat%C3%A1strofes Wikipedia.org. (2024) Sistema Dinamico. Wikipedia. https://es.wikipedia.org/wiki/Sistema_din%C3%A1mico Lacasta Codorniu, M. (2020) Teoría de las Catástrofes | Miquel Lacasta. Veredes. https://veredes.es/blog/teoria-de-las-catastrofes-miquel-lacasta/ Diez de Ulcurrun, F. (2017) TEORÍA DE LAS CATÁSTROFES. Estancias Egonaldiak. https://centrohuarte.es/blogh/2017/11/12/teoria-de-las-catastrofes/ Hercer Editorial S.L. (2024) Catástrofes, teoría de las. Enciclopedia Herder. https://encyclopaedia.herdereditorial.com/wiki/Cat%C3%A1strofes,_teor%C3%ADa_de_las wikipedia.org (2023) René Thom. wikipedia. https://es.wikipedia.org/wiki/Ren%C3%A9_Thom Nebula, C. (2023). Swallowtail catastrophe animation gif [imagen] Extension:Media Viewer https://upload.wikimedia.org/wikipedia/commons/4/41/Swallowtail_catastrophe_animation_gif.gif Konrad, J (1970). Mathematician René Thom in Nice [fotografia] oberwolfach Photo Collection https://opc.mfo.de/detail?photo_id=4170 Deleuze, G (2023). El pliegue [imagen] factordestiba.blogpost.com. https://3.bp.blogspot.com/_ZPFzMY4_o_w/TLn5wuHZfRI/AAAAAAAAAGw/KyN855IIiyo/s400/Thom_discontinuidad.GIF 1freewalpapers.com (2018) volcan [Imagen] 1freewalpapers.com https://1freewallpapers.com/volcano-lava-sparks-cracks-balloon/es