
La Teoría de las catástrofes.
Catástrofe:
La Teoría de las catástrofes, Cuando se habla de catástrofes nos referimos a aquellos hechos que suceden de forma inesperada y de forma discontinua, se habla también de diferentes fenómenos de los cuales no podemos deducir de manera exacta.
El termino suele ser relacionado con desastres naturales pero no solo se aplica a este campo, si no que esta teoría fomenta estudios científicos que se encuentran en la cotidianidad.
Este término se trabajó por primera a finales de la década de 1950 por el matemático francés René Thom, es considerado como uno de los fundadores de la tipología diferencial además de establecer la teoría de las singularidades.
Rene Thom fue mayormente conocido por la teoría de las catástrofes e hizo que se reconociera en el campo estrictamente matemático sin embargo también fue reconocido en otros campos diversos como la economía la biología o las ciencias sociales.
La catástrofe como una teoría:
Podemos entender que la teoría de las catástrofes logra explicar o demostrar los diferentes sistemas estructurales y como estos pueden presentar cambios inesperados en el comportamiento
Esta teoría tiene su aplicación inmediata a los sistemas matemáticas los cuales tienen un sistema de alta fricción que obedece a la ley de Aristóteles (La velocidad es proporcional a la fuerza el cual nos indica que el sistema del que se habla tiende a un estado estacionario o a uno equilibrado.
La TC tiene un gran atractivo debido a su representación visual, que nos muestra gráficamente la caracterización de los diferentes sistemas. Esto es posible si suponemos que el estado en la que se encuentra el sistema esta descrito por una variable en un plano sea x o y.
Caracterización de la teoría de las catástrofes:
Este fenómeno maneja dos compresiones muy complejas acerca de varios fenómenos que conforman esta, en la que encontramos:
- Fluctuaciones: Se presentan diferentes variables en determinadas mediciones de un sistema constante.
- Impredecibilidad: Se refiere a aquellos eventos o situaciones que carecen de un patrón, por lo que no se puede anticipar o anticipar los movimientos de un sistema.
- Emergencia: Se genera a partir de una conexión que origina una novedad en el sistema considerado como un todo.
- autoorganización: Se caracteriza por la conducta compleja de sistemas físicos, biológico y sociales que después de alcanzar cierto tamaño expresan un nuevo comportamiento que no puede ser clasificado por las características locales de los elementos.
- Discontinuidad: Se produce por los cambios repentinos en cuanto a comportamientos o resultados, este es producido por la inestabilidad de un estado lo que produce fuertes incongruencias que conllevan a un cambio fuerte.
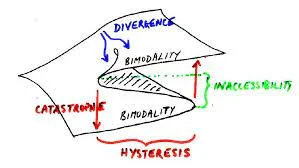
- Divergencia: Son variaciones frecuentes que a medida que pasa el tiempo se producen cambios mas alargados que los del punto inicial.
- Histéresis: Este fenómeno consiste en una serie de cambios, pero a diferencia de las otras definiciones esta es irreversible y los comportamientos no le permiten regresar a su estado inicial.
Criticas y controversias de la teoría de las catástrofes:
- Aplicabilidad limitada: Se argumenta que su aplicabilidad es limitada al no ser directamente relacionado con muchas situaciones del mundo real
Sin embargo, se ha demostrado que, aunque en principio haya tenido un objetivo en fenómenos físicos y biológicos llegaron a campos como la biología, la ecología y la psicología, incluso en la actualidad sigue siendo relevante ya que por medio de esta teoría se ha utilizado también en inteligencia artificial para modelar fenómenos complejos o simplemente para analizar cambios bruscos en el rendimiento de algoritmos por lo que esto considera una aplicación mas amplia de la que se consideró.
- Sensibilidad a los parámetros: Esta afirmación refiere a la compleja medición que esta requiere ya que con un mínimo margen de error se pueden mostrar resultados totalmente diferentes a los esperados.
En cuanto a este punto si hay muchas afirmaciones validas ya que en situaciones donde se requiera un cien porciento de efectividad de las predicciones pude llegar a tener muchas limitaciones.
- Complejidad de los modelos: La teoría de las catástrofes requiere de modelos muy complejos por lo que muchos críticos hacen referencia a que sea menos accesible cuando se pueden implementar sistemas más simples.
Sin embargo, este tipo de modelos es de gran ayuda en situaciones dónde se requiera analizar de otros tipos de sistemas más complejos y sobre todo que no sean lineales.
Como podemos observar la mayoría de estas características va relacionado con los cambios sorpresivos e impredecibles que tiene muchas funcionalidades, que sirven de utilidad para poder comprender enigmas como la divergencia de sistemas, que va correlacionado con los sistemas complejos.
¿Qué es un sistema complejo?:
Un sistema complejo suele ser de forma creciente esto hace que se caractericen por tener dinámicas irreversibles, súbitas, imprevisibles, aperiódicas.
Los sistemas complejos están compuestos por muchos elementos que pueden interactuar entre sí, donde si llega el caso de querer estudiar parte por parte por separado no se tendría el comportamiento en general de un sistema determinado.
Entre estos sistemas podríamos encontrar un ejemplo claro, como vendría siendo el cerebro conformado por millones de células que vendrían siendo los elementos individuales, que cuando interactúan entre estas producen las propiedades cognitivas del cerebro como podría ser la memoria.
En estas investigaciones de sistemas complejos se desarrollaron varias herramientas que permiten el estudio de estas como lo son las redes complejas en las que cada elemento individual se considera conectado con otros sea directa o indirectamente.
Para los sistemas complejos todos los elementos del sistema van entrelazados y esto hace que sea muy difícil lograr separarlos esto en casos en los que las interacciones de sus componentes sean relevantes.
Podemos decir que los componentes son relevantes a medida que estos que determinen parcialmente el futuro de los componentes; Un ejemplo de esto seria una partida de ajedrez donde los elementos serias los movimientos que se realicen, es decir que los movimientos futuros dependerán de las acciones que realice el rival.
Su relación con la teoría de las catástrofes se produce a medida que conocemos información nueva que no esta presente en las condiciones iniciales lo que dificulta a gran medida el que tanto podremos predecir.
Campos en los que aplica la teoría de las catástrofes:
Esta teoría ha tenido campos de acción desde solo haberse visto en el área de matemáticas hasta encontrarse en campos como la Física, la biología, las ciencias sociales, la lingüística, etc.…
También demuestra una correlación a la teoría de la singularidad que a través de la función de Liapunov podemos analizar y detallar el equilibrio estacionario en algunos sistemas por lo cual podemos deducir que la teoría de las catástrofes tiene como base un sistema complejo.
Esto quiere decir es que a partir del modelo dinámico mas simple es posible comprenderla por medio de herramientas matemáticas que puedan proporcionar una descripción empírica de los fenómenos que se consideren discretos.
¿Los sistemas complejos pueden ser lineales?:
Para resolver esta pregunta lo resolveremos analizando un aura de simetría, donde en principio hay un caos esto debido a la falta de una relación de causa y efecto lo que producen los futuros impredecibles que en un principio tendrían un orden no lineal, ya que este sería un orden oculto en el que se encuentra la incertidumbre absoluta.
Sin embargo, a medida que pasa el tiempo podemos observar que se comienzan a formar normas que sean capaces de regular el abuso lo que hace que el aura de simetría que hasta el momento era complejo se empiezan ver características de forma lineal o también como sistemas complicados.
La causa efecto separado en tiempo y espacio demuestra lo complicado que puede llegar a ser.
¿Quién fue René Thom?:
El matemático francés trabajo en el campo de la topología además integro el cobordismo pero el aporte mas importante hasta el momento fue a la teoría de las catástrofes.
Se considera uno de los fundadores mas importantes de las matemáticas modernas debido a la relación que se ha originado con la teoría del caos.
En su obra más representativas “La teoría de las catástrofes” cosiste en afirmar que en un sistema continuo se puede producir espontáneamente uno discontinuo.
El cual por medio de su razonamiento buscaba prever algunos acontecimientos como lo pueden ser el estallido de una ola, los motines de una prisión o las crisis económicas que pudieron haber precedido para encontrar una solución anticipada por medio de esta.
Tipos de catástrofe:
- Catástrofe de Cúspide: En esta podemos encontrar un punto en el cual una variación en algún parámetro del sistema podría producir una divergencia
- Ejemplo: Esta la podemos representar por medio de una esfera rodando en una superficie cónica, cuando esta llegue al vértice de la cúspide una divergencia podría ocasionar movimientos a diferentes lados, por lo que no sabremos con certeza cual es el camino que tomara.
- Catástrofe de Pliegue: A diferencia de la anterior hay cambios en la forma en la que se produce la divergencia ya que esta describe un cambio de manera repentina y menos brusca.
- Ejemplo: Consideremos para este ejemplo una hoja de papel delgada y flexible, Se podría doblar de distintas formas diferentes sin embargo llega un caso en el que el comportamiento de esta por hacer un pequeño ajuste se pliegue de una manera repentina ahí entraría esta catástrofe.
- Catástrofe de Cola de Golondrina: Como su nombre lo indica esta cuenta con la forma de una golondrina la cual consta de varios parámetros y a diferencia de las anteriores estas se caracterizan por varios puntos de divergencia
- Ejemplo: Se puede imaginar una ecuación matemática las cuales tienen varios puntos y cuando algunas variables cambian es donde se producen las divergencias.
Estas tres son las principales sin embargo podemos encontrar más como la mariposa, el ombligo parabólico, el ombligo elíptico, el ombligo parabólico y el ombligo hiperbólico que, así como las anteriores buscan una manera de definir todas las catástrofes y como se producen.

Conclusión:
Como reflexión final esta teoría a demostrado ser de gran utilidad cuando queremos evaluar las predicciones o los posibles cambios tanto simples como bruscos de un sistema además de tener una amplia perspectiva en múltiples campos de las ciencias e investigación.
Aunque tenga muchos desafíos como la complejidad de los modelos evaluados o los datos extremadamente precisos que se requieren, esta ha tenido una aplicación efectiva y ha mantenido un equilibrio entre las matemáticas y la vida cotidiana.
Teniendo en cuenta las afirmaciones anteriores la Teoría a revolucionado la manera de ver los sistemas no lineales y seguirá siendo un modelo útil incluso con las nuevas ciencias y nuevos campos .
Créditos:
Autor: Sebastian Alvarez
Editor: Carlos Iván Pinzón Romero
Código:UCPSG5-1
Universidad: universidad central
portada: https://www.google.com/search?q=catastrofes+matematicas+1280+x720+p&tbm=isch&ved=2ahUKEwjQiP6MyMWEAxUZv4QIHSl9CIMQ2-cCegQIABAA&oq=catastrofes+matematicas+1280+x720+p&gs_lp=EgNpbWciI2NhdGFzdHJvZmVzIG1hdGVtYXRpY2FzIDEyODAgeDcyMCBwSMwoUOoEWJcmcAB4AJABAJgBzAKgAdcQqgEIMC4xMC4wLjO4AQPIAQD4AQGKAgtnd3Mtd2l6LWltZ8ICBBAjGCeIBgE&sclient=img&ei=3rXaZdChM5n-kvQPqfqhmAg&bih=931&biw=1024#imgrc=vz-og44Vlk8O5M Imágenes: https://www.google.com/search?q=teoria+de+las+catastrofes+720+x+1250&tbm=isch&ved=2ahUKEwjCu5zT1cGEAxX0BWIAHbV8BXYQ2-cCegQIABAA&oq=teoria+de+las+catastrofes+720+x+1250&gs_lp=EgNpbWciJHRlb3JpYSBkZSBsYXMgY2F0YXN0cm9mZXMgNzIwIHggMTI1MEiMFlDeBVidE3ABeACQAQCYAXygAZ8FqgEDMC42uAEDyAEA-AEBigILZ3dzLXdpei1pbWfCAgQQIxgniAYB&sclient=img&ei=NKvYZcLRM_SLiLMPtfmVsAc&bih=922&biw=2023&hl=es-419#imgrc=ikAA2bX-1s7oqM https://www.google.com/search?sca_esv=1a30264c0409ca1f&sxsrf=ACQVn0_fde0shqJFs8X6JGuGJrW2qqS-kw:1708698830371&q=rene+thom&tbm=isch&source=lnms&sa=X&ved=2ahUKEwinwb-W18GEAxUPLtAFHQkGDjcQ0pQJegQIFhAB&biw=2049&bih=922&dpr=0.67#imgrc=ilpvUbFqEkhHKM https://www.google.com/search?sca_esv=23bfc37b28131238&sxsrf=ACQVn08ncOBFtXeEIn4OHPUb5gs0SwkSDQ:1708830796416&q=teoria+de+las+catastrofes&tbm=isch&source=lnms&sa=X&ved=2ahUKEwiQ2-fkwsWEAxVkVTABHVUgCZcQ0pQJegQIGhAB&biw=2049&bih=922&dpr=0.67#imgrc=8IgvNx1da_yoHM https://www.google.com/search?q=teoria+de+las+catastrofes&sca_esv=23bfc37b28131238&sxsrf=ACQVn0_5kLhizNEjZY6WRpj2iuO6e9VvmQ:1708831424234&tbm=isch&source=iu&ictx=1&vet=1&fir=8IgvNx1da_yoHM%252CYbi4SKVPKKhVFM%252C%252Fm%252F02810f%253BikAA2bX-1s7oqM%252CdBRyuWbs3E69DM%252C_%253Bk3VQiXEO2xZo5M%252CYbi4SKVPKKhVFM%252C_%253BxxG2Ada3vaAbBM%252CL9irr-TD87iSDM%252C_%253B14dEmDQqOJuerM%252CjFT4lnUQk0eTlM%252C_&usg=AI4_-kT0YUWDfspN8Di5whhG7h6dhTziPA&sa=X&ved=2ahUKEwiQ15aQxcWEAxXjbDABHZoRBfMQ_B16BAhYEAE#imgrc=8IgvNx1da_yoHM Información: (Departamento de Física, cubículos, 2020)https://www.revistacienciasunam.com/pt/168-revistas/revista-ciencias-20/1502-teor%C3%ADa-de-cat%C3%A1strofes. (Maldonado Carlos, 2006)lhttps://www.redalyc.org/pdf/532/53200304.pdf (Castillo Ramon, 2014)https://www.redalyc.org/pdf/836/83642664002.pdf (Maldonado Carlo,2014)https://www.redalyc.org/pdf/414/41438646004.pdf https://www.ecured.cu/Ren%C3%A9_Thom








