
Sistema Octal
Es un sistema de numeración en base 8 lo que significa que tiene ocho dígitos posibles: 0, 1, 2, 3, 4, 5, 6, 7. Por lo tanto, cada dígito de un número octal puede tener cualquier valor de 0 a 7. El sistema octal se utiliza con frecuencia en el trabajo de computadoras digitales. Este sistema tiene una ventaja y es que se puede simplificar dígitos grandes del sistema binario.
Historia del sistema octal
Tiene su origen en la antigüedad, cuando las personas usaban sus manos para contar de ocho en ocho los animales. Existe la posibilidad de que en la antigüedad se usará el sistema de numeración octal antes que el decimal para poder contar los espacios interdigitales; es decir, contar todos los dedos a excepción de los pulgares. Este sistema numérico fue creado en el siglo XVII por el alemán Gottfried Leibniz quien publicó un artículo titulado Explicación de la Aritmética Binaria.
Posteriormente se estableció el sistema de numeración octal, que se originó a partir del sistema binario, porque este necesita de muchos dígitos para representar sólo un número; a partir de entonces se crearon los sistemas octales y hexagonales, que no requieren de tantos dígitos y que fácilmente pueden convertirse al sistema binario.
Figura 1

Nota. Dígitos utilizados en el sistema numérico octal. (TREMBLAY, 2014). https://eldiscretini.wordpress.com/sistema-octal/
Características del sistema octal
Cuando se llega a 7 devuelve a 0 para el siguiente conteo; de esa forma se incrementa la siguiente posición del dígito. por ejemplo, para contar en el sistema octal sería:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 20, 21, 22, 23, 24, 25, 26, 27, 30
- 40, 41, 42, 43, 44, 45, 46, 47, 50.
En la siguiente Tabla 1 se expresan los números decimales y su conversiones:
Ventajas del sistema octal
- No requiere utilizar otros símbolos diferentes de los dígitos.
- Es usado en la computadora para abreviar los números binarios grandes.
- Este sistema permite una fácil conversión de binario a octal y viceversa.
Desventajas del sistema octal
- Está limitado a una cantidad de siete dígitos que van del 0 al 7.
- No se utiliza en la cotidianidad para expresar cantidad debido a su ineficiencia de no poseer los números 8 y 9 y debido a su nivel de interpretación.
Tabla 1
conversión entre los distintos sistemas numéricos

Nota. Los dígitos de los sistemas numéricos. D’Alessio, V. (2021). Sistemas numericos. Recuperado de: https://elibro-net.ezproxy.ucentral.edu.co/es/ereader/biblioucentral/48716?page=46
Conversión del sistema octal a otros sistemas numéricos
Octal a Decimal
Figura 2
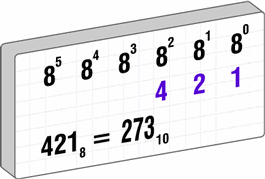
Nota. Convergencia del sistema octal al sistema decimal (HARDWARE, 2020). Sistema hexadecimal. Obtenido de:https://sites.google.com/site/tema2informatica1btx/datos-e-informacion/sistema-de-numeracion-octal-hexadecimal
Un número octal se puede convertir rápidamente a su equivalente decimal multiplicando cada número octal por su peso posicional. Ejemplo:
- 3828 = 4 * (82) + 8 * (81) + 2 * (80)
- = 3 * 64 + 8 * 8 + 2 * 1
- = 25810
Octal a Binario
La conversión de octal a binario se realiza convirtiendo cada dígito octal a su equivalente binario de tres dígitos. En la tabla 1.1 se muestra como se convierten los ocho posibles dígitos.
A partir de esas conversiones se puede cambiar cualquier número del sistema octal al binario. Por ejemplo:
- 6 = 110
- 4 = 100
- 7 = 111
Por lo tanto, 647 equivale en el sistema binario a 110100111.
Octal a Hexadecimal
Para convertir un dígito octal al sistema hexadecimal o viceversa es necesario que primero se convierta el número en binario, y luego al sistema deseado.
Convertir el número octal 1542 en un número hexadecimal:
Se convierte el número de octal a binario
1 = 1
5 = 101
4 = 100
7 = 111
Así, 1547=1101100111
Para convertir de binario a hexadecimal primero se ordenan en grupo de 4 bits, empezando de derecha hacia izquierda:
11 0110 0111 – Se completa con ceros el primer grupo, para que este pueda tener 4 bits:
0011 0110 0111 – Se hace la conversión del sistema binario al hexadecimal. Se sustituyen las equivalencias por medio de la tabla
0011 = 3
0110 = 6
0111 = 7
De esa forma, el número octal 1547 equivale a 367 en el hexadecimal.
Conclusiones
- El sistema numérico octal es uno de los más fáciles a comparación de los demás sistemas numéricos ya que simplifica dígitos grandes como los binarios.
- Este sistema numérico tiene una gran ventaja y es que es más fácil de manejar ya que no incluye otros símbolos aparte de los 8 dígitos.
- A través del tiempo se ha utilizado los diferentes sistemas numéricos. Como los granjeros en la antigüedad lo utilizaban para contar los animales. Ahora en la actualidad se utilizan en la informática.
Autor: Nikson David Zarate Parra
Editor: Ing. Carlos Ivan Pinzon Figueroa
codigo: UCPA-6
Universidad: Universidad Central
Fuentes:
Rodríguez, D. (2010, August 2). Daniel Rodríguez Herrera - Los inventores de los ceros y unos. Libertad Digital. Retrieved February 19, 2023, from https://www.libertaddigital.com/opinion/agosto/los-inventores-de-los-ceros-y-unos-1276238076.html
D'Alessio, V. (2021, April 14). Sistema octal: concepto, sistema de numeración, ejemplos. Lifeder. Retrieved February 19, 2023, from https://www.lifeder.com/sistema-octal/
Castro, M. (2014). Estructura y tecnología de computadores I (Gestión y Sistemas). UNED - Universidad Nacional de Educación a Distancia. https://elibro-net.ezproxy.ucentral.edu.co/es/ereader/biblioucentral/48716?page=46
Rodríguez, D. (2010, August 2). Daniel Rodríguez Herrera - Los inventores de los ceros y unos. Libertad Digital. Retrieved February 19, 2023, from https://www.libertaddigital.com/opinion/agosto/los-inventores-de-los-ceros-y-unos-127623os-inventores-de-los-ceros-y-unos-1276238076.html
HARDWARE. (09 de 10 de 2020). Obtenido de Sistema numericos: https://sites.google.com/site/tema2informatica1btx/datos-e-informacion/sistema-de-numeracion-octal-hexadecimal









Pingback: Sistema Numérico Hexadecimal. -
Pingback: Sistema numérico decimal - Computación Gráfica