LA TEORIA EL CAOS Y EL EFECTO MARIPOSA
Para Comenzar Es Pertinente Ahondar Sobre Que Es Esta Teoría
Estudiada a profundidad por el pionero James A Yorke profesor de física y matemáticas en la universidad de Maryland en estados unidos. Interpretamos la teoría del caos como el hecho de que un pequeño cambio realizado en una actividad. Puede desencadenar todo un conjunto de hechos, que no habrían ocurrido sin este pequeño cambio.
Este demostró que la aparición de un ciclo de tres puntos en un sistema dinámico. Seria un indicio de que el sistema puede mostrar un comportamiento caótico.
Lo cual fue de suma importancia en esto, puesto que se logra una relación matemática entre estos. Y se percibe como puede existir una relación entre la complejidad y el caos. De igual modo Yorke con sus diversos experimentos contribuye al entendimiento de los patrones caóticos que podrían presentar los sistemas naturales y artificiales
Así mismo alguna vez hemos escuchado hablar del efecto mariposa lo cual es básicamente perteneciente a esta teoría. Puesto que es una metáfora de que el aleteo de una mariposa podría ocasionar un tornado. Refiriéndose así que cualquier variación por pequeña que parezca puede ocasionar diferencias muy significativas en un sistema a largo plazo en el mismo.
Aplicación de la teoría del caos
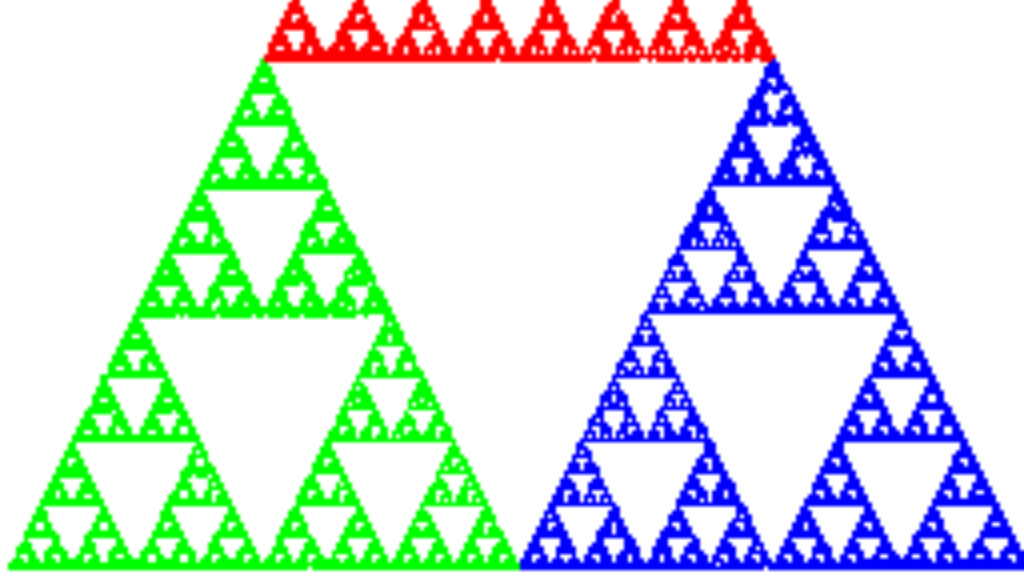
Esta teoría puede ser visualizada como un acontecimiento en; por ejemplo, un simple juego titulado “El juego del caos”. Que consiste en una hoja de papel en la cual en los extremos tendrá demarcado los números del 1 al 6 por pares. Para ser jugado con un dado o una secuencia de números al azar en ese rango. Es decir, tendrá 3 puntos iniciales, luego se debe elegir un punto de partida al azar en la hoja.
Al lanzar el dado se debe unir con una línea hasta la mitad del punto inicia. En dirección a donde se encuentre el numero que sale en el dado.
Y desde ese punto se repite la acción para obtener otra dirección con cada lanzamiento del dado. Y lo verdaderamente increíble es que si este procedimiento se repite muchas veces no quedara en la hoja un desorden de puntos. En caso contrario queda plasmado una estructura geométrica increíblemente ordenada.
Lo que nos lleva a identificar que desde el aparente caos se puede dar algo absolutamente maravilloso. Este simple juego nos permite comprender un poco que tan sensible resulta el echo de las condiciones iniciales. Al elegir un punto completamente al azar, pero siempre permitiendo esta estructura ordenada al final

Y esta teoría es importante para ayudarnos a comprender sobre distintos temas y el cómo funcionan ciertas cosas en el mundo. En ámbitos de física, medicina, biología. Por ejemplo, uno de los temas más nombrados en donde podemos contemplar a que se refiere esta teoría es el sistema solar. Puesto que es algo que siempre a intrigado a la humanidad y lo que nos lleva a cuestionarnos si quizá. ¿Al conocer suficientes datos podríamos llegar a predecir cosas puntuales y hasta el futuro?.
Sin embargo, hay que tener en cuenta la predicción Newtoniana en donde para Newton el símbolo que mejor representa esta predicción es el reloj. Debido a que este marca el tiempo de una manera suave y regular. No obstante al profundizar en lo no lineal se conjetura que incluso los sistemas mas sencillos serian imposibles de predecir.

¿A Que Se Le Llama Lo No Lineal?
A esto nos referimos que un pequeño cambio puede ocasionar un gran evento. Por ejemplo como ocurriría con una plataforma en la que ubicamos 1 kg de material. Y seguidamente agregamos 1 kg más y al caer una pequeña espiga esta plataforma se desploma.
Relevancia De La Teoría
Nos permite estudiar diferentes sucesos en el mundo puesto que los sistemas caóticos resultan en temas muy complejos como lo es la ingeniería. Pues al presentarse vibraciones en elementos y no poder predecirlas complica que un ingeniero pueda anticipar si está creando una estructura segura. O en el caso de la meteorología debido a que al analizar el comportamiento del clima las precipitaciones, la humedad. Podría tener un comportamiento tan variado aparentemente sin ningún objetivo.
Así mismo como ocurre en el ámbito de la medicina con un electrocardiograma o en las imágenes de ondas cerebrales. No obstante, el punto especifico de esta teoría es el hecho de que al presentarse un ínfimo cambio en el sistema que se este estudiando en cualquiera de las ramas mencionadas permite que la investigación cambie por completo y demuestre diferentes patrones por ello se realiza tanto énfasis en que el punto de partida puede transformarlo todo. Lo cual resulta extremadamente importante pues de no haber realizado estudios de esta teoría se podrían perder muchas investigaciones debido a que los científicos habrían considerado los experimentos erráticos.
El Caos Como Revolución Científica
Uno de los pioneros de la teoría del caos Edward Lorenz a quien se le adjudica la metáfora del efecto mariposa, descubrió en 1961 los atractores extraños que son los sistemas cuyo comportamiento no se rige por constantes o periódicos, ni aleatorios así muchas veces lo parezca estos se rigen por normas profundas.
Puesto que las trayectorias de 2 partículas cercanas pueden ser desiguales debió a su punto de partida e incluso puede verse como una combinación entre el orden y el caos a causa de que la complejidad que presentan se repite una y otra vez, pero a diferentes escalas, a esto se le conoce como fractal.
Se pueden encontrar diversos atractores extraños; el descubierto por Lorenz es usado en la certeza atmosférica y tiene forma de hélice o alas de mariposa

Otro de los atractores seria el conjunto de Mandelbrot, siendo este un conjunto de fractales importante en la ciencia y el arte para el estudio de la autosimilitud y geometría fractal. Y por último el atractor de Rossler muestra una estructura fractal, usado ampliamente para el estudio de sistemas dinámicos de baja complejidad.
Sin estos atractores seria extremadamente difícil comprender el caos y como los cambios realizados en las condiciones presentes alteran en gran media los resultaos de los mismos en algunos sistemas puesto que facilitan la exhibición del comportamiento y evolución de estos como lo son la dinámica de fluidos, el clima, las dinámicas en biología.
El meteorólogo Lorenz observo mediante una investigación realizada para determinación de procesos atmosféricos con la ayuda de la tecnología presente para la época y por cuestiones de tiempo al no iniciar en el mismo punto de partida si no por el contrario a mitad del recorrido a una hora de transcurrido el experimento sin ningún cambio adicional a como siempre se realizó este se había desarrollado de manera diferente sin embargo siendo cercana a la primera secuencia. Comprendiendo así que al momento del registro de los datos el hecho de haber omitido tres decimales lo que le permitió evidenciar este nuevo atractor descubierto; debido a que reconocidos se encontraban la dona el ciclo limite y el punto fijo. Todos en relación a sistemas la primera a uno cuasiperiódico el segundo a un sistema periódico y el ultimo a uno constante.
Se llega a ver como una revolución científica debido a que en ese momento se buscaba constatar el predecir los sistemas y esta teoría dio paso a una percepción totalmente diferente.
Así mismo el meteorólogo Edward Lorenz no fue el único que realizó investigaciones sobre el tema puesto que años atrás filósofos y matemáticos habrían expresado conjeturas similirares en sus escritos sin embargo Lorenz logro visualizar ese aparente error matemático como lo que es hoy en día, cuyos estudios a esta no se han detenido, y han llevado a la evolución y desarrollo de un sinfín de sistemas y por qué no podrían llegar a predecirse, a pesar de que resulten aparentemente simples, muestras un resultado complejo, lo que no habría sido posible sin la aplicabilidad a sistemas no lineales pues estos cambian la estructura y son sensibles a las condiciones iniciales pues de esto dependerá del punto en donde finalice el sistema determinando así su trayectoria.
Cabe aclarar que cuando hablamos del caos no representa la equivalencia a no estructuración de los sistemas, si no a algo impredecible o aleatorio que erróneamente se tiene a percibir como desordenado y llega a ser todo lo contrario incluso hasta positivo un orden difícil de anticipar, desafiando así la idea de que únicamente los sistemas lineales podrían tener una armonía en donde se visualizan patrones y estructuras sumamente interesantes por ejemplo, en el campo de la medicina es necesario que se presente ese caos en los electrocardiogramas al monitorear el corazón o en las ondas cerebrales en donde ver ondas ordenadas y parejas podrían representar condiciones patológicas peligrosas.
El estudio de esta teoría permite a los médicos prever y tratar estas condiciones, por medio del modelado no lineal e los sistemas biológicos de la enfermedad y el avance de la misma. De este modo lo anterior nos lleva a pensar que quizá el universo requiere de este caos para un correcto funcionamiento sin necesidad de ser relacionado con algo negativo o que se deba a corregir.

CREDITOS:
Autor: Maira Alejandra Acuña Rodríguez
Editor: CAMILO ORTIZ
Código: UCPAG4-3
Universidad: Universidad Central
FUENTES
Universidad de Murcia. (s.f.). Edward Lorenz: Pionero de la teoría del caos. En Docencia de la Universidad de Murcia. Tomado de https://www.um.es/docencia/barzana/BIOGRAFIAS/Biografia-Edward-Lorenz.php
Varona, J. L. (2017, diciembre 5). Edward Lorenz (1917-2008): con él empezó el caos. Blog del Instituto de Matemáticas de la Universidad de Sevilla. Tomado de https://institucional.us.es/blogimus/2017/12/edward-lorenz-1917-2008-con-el-empezo-el-caos/
Stewart, Ian (2001), ¿Juega Dios a los dados? La nueva matemática del caos. traducción de M. Ortuño, J. Ruiz Martínez et al., Barcelona, España, Editorial Crítica.
Álvarez, M. (2014). La creación de la metáfora: El efecto mariposa. Ciencia, Academia Mexicana de Ciencias, 65(2), 36-41.







