
Mitchell Feigenbaum “Buscar el orden en el caos”
Mitchell Feigenbaum
Fue un matemático, físico estadounidense nacido el 19 de diciembre de 1844 en Filadelfia, Pensilvania, sus estudios fueron centrados en “teoría del caos” teoría la cual desenlazo el descubrimiento de los números de Feigenbaum.
Inicio sus estudios en el instituto Samuel J. Tilden High School ubicada en Brooklyn y City College de Nueva York, realizo su tesis sobre las relaciones de dispersión con el acompañamiento del profesor Francis E. Low
En 1975 Feigenbaum descubrió sobre la proporción de diferencias entre los valores que se dan en estos subsecuentes ciclos de duplicación, bifurcación que tienden a un valor constante de 4,6692 , este trabajo se logró efectuar gracias al ordenador HP-65, debido a esto obtuvo una demostración matemática sobre dicho caso, luego demostrando que con la propia constante matemática se produce la misma conducta antes del inicio del caos para una extensa clase de funciones matemáticas ya obtenida esta variable universal se le permitió a los matemáticos dar los primeros pasos hacia el juicio del comportamiento aparentemente aleatorio del sistema caótico a esta proporción de convergencia ahora se le llama la primera constante de Feigenbaum.
Números de Feigenbaum
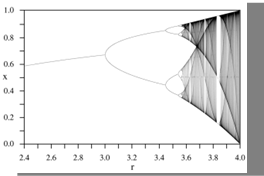
Los números de Feigenbaum o constantes de Feigenbaum son dos números reales descubiertos por el matemático en los cuales ambos expresan cocientes que aparecen en los diagramas de bifurcación en la teoría del caos.
Los diagramas de bifurcación enlazan a los valores extremos que toma una secuencia del tipo
Xռ+1=µƑ(Xռ) en donde Ƒ es una función real positiva y a su vez tres veces derivable sobre [0;1] y tomando el único valor máximo sobre ese intervalo , considerando Xռ para una función determinando el valor de µ la secuencia conduce a un único límite sobre ese valor , Los valores de µ que separan dos intervalos son llamados valores de las bifurcaciones y se nombran como µ1, µ2
La primera constante está definida como:
4,669 201 609 102 990 671 853 203 821 578 439…
Feigenbaum y la teoría del caos
El caos fue un tema de esplendor a mediados de la década de 1980. Muchas universidades y centros de investigación han establecido grupos que se especializan en dinámica no lineal y sistemas complejos. Términos como bifurcación (cuando un pequeño cambio en el valor de un parámetro de un sistema provoca un repentino cambio “cualitativo” o topológico en su comportamiento), fractal (una imagen del caos) o el efecto mariposa se están extendiendo rápidamente.
Matemáticos, pero también meteorólogos, antropólogos, sociólogos, físicos, filósofos, informáticos, ingenieros o economistas quieren mirar más allá del desorden aparentemente aleatorio de la naturaleza para buscar el comportamiento de los mercados financieros, fenómenos meteorológicos, conocidos La conexión entre los movimientos de la evolución de los ecosistemas de algunos cuerpos celestes…
La teoría del caos se convierte en una herramienta matemática ideal para extraer estructuras ordenadas de mares caóticos. Se basa en dos ideas principales:
1) incluso los sistemas complejos contienen orden fundamental.
2) en tales sistemas, pequeñas diferencias en las condiciones iniciales (como pequeños cambios de temperatura) pueden conducir a resultados muy diferentes.
lo que significa que es imposible generalizar su comportamiento para predecir a largo plazo, matemáticamente decimos que el sistema tiene una fuerte dependencia de las condiciones iniciales. Esto sucede incluso si el comportamiento de estos fenómenos está completamente determinado por sus condiciones iniciales, sin la participación de ningún factor aleatorio. En otras palabras, el determinismo de estos sistemas no los hace predecibles, aunque al menos gracias a la teoría del caos podemos analizar su imprevisibilidad desde un punto de vista estratégico.
Pensamiento de Feigenbaum
Al ser un matemático, físico tiene una forma de pensar diferente o también piensan diferente en temas poco frecuentes, este matemático que dio su vida a trabajar en la teoría del caos definió su pensamiento a esta frase.
“También el caos tiene sus normas”
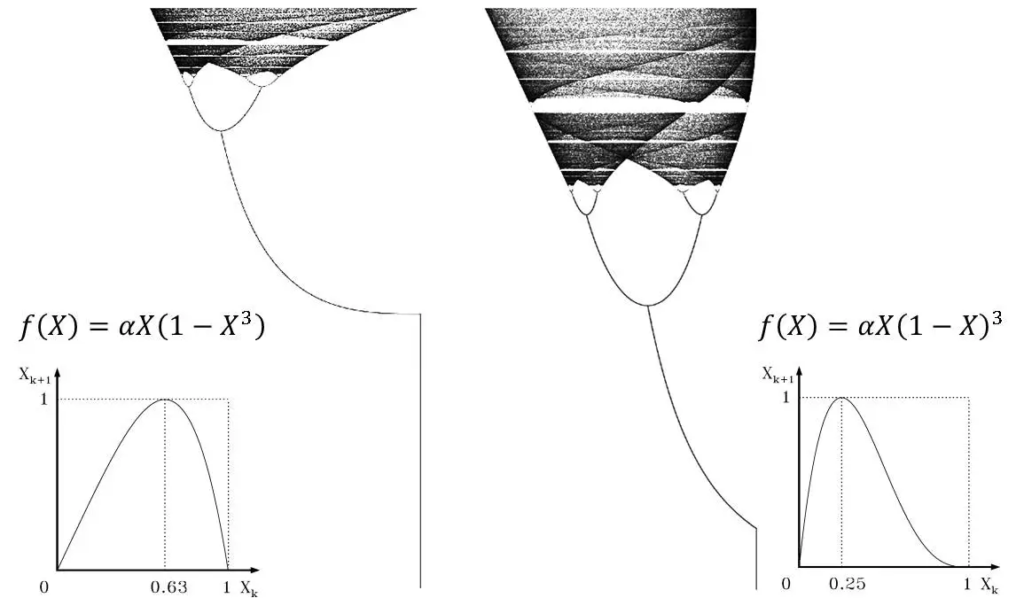
2.2 Teoría del Caos
En general, la teoría del caos estudia la sensibilidad de ciertos sistemas a las condiciones iniciales, es decir, aquellos sistemas en los que pequeños cambios pueden tener grandes consecuencias. Matemáticamente, estos cambios siguen dinámicas no lineales.
2.3 Donde se aplica la teoría del caos
La teoría del caos general mente se aplica a lo que es llamado “sistemas dinámicos”.
Un sistema dinámico es una serie de sucesos que varían o cambian con el tiempo como por ejemplo una población o la degradación que puede tener una fruta con el pasar del tiempo
2.3 Donde se produce la teoría del caos
En teoría se puede decir que el caos comienza cuando se crean diferencias en el estado inicial esas diferencias creando un estado final.

2.4 Como se clasifica la teoría del caos
La teoría del caos es una rama de las matemáticas, la física y otras ciencias (incluidas la biología, la meteorología y la economía) que se ocupa de ciertos tipos de sistemas dinámicos complejos y no lineales que son muy sensibles a los cambios en las condiciones iniciales.
2.5 Teoría del caos y Edwar Lorenz
En 1963 Edwar trabajaba en un proyecto basado en unas ecuaciones las cuales predijeran el tiempo en la atmosfera y para poner aprueba sus ecuaciones la plasmaba en un computador, Edwar se sorprendió al ver que, con una simple variación de 3ª6 decimales puede crear una gran diferencia en las predicciones del modelo, en conclusión una pequeña variación puede causar un gran cambio en el resultado final del modelo
2.6 Teoría del caos en el pensamiento sistémico
La teoría del caos establece que el mundo no sigue patrones fijos y predecibles, sino que opera de manera caótica, los procesos y el comportamiento están determinados en gran medida por circunstancias inciertas.

Básicamente, muestra que una gran clase de sistemas que en algún momento experimentan una transición de un comportamiento regular y predecible a un comportamiento caótico e impredecible y que el proceso de transición es universal.
Dejando en claro que la naturaleza y el universo esta en un estado inicial de caos pero que a su vez ese mismo caos genera un orden dentro de él, ya que el orden se oculta tras en desorden y lo aleatorio siempre esta en juego ya que nada es lineal.
Créditos:
Autor: Bryan Sebastian Toro Cruz
Editor: Carlos Iván Pinzón Romero – Luisa Fernanda Zambrano Garcia
Código: UCPSG6-1
Universidad: universidad central
Fuentes:
Oscar Menéndez (s/f) https://www.muyinteresante.es/ciencia/6487.html M macho (19/12/2014) https://ztfnews.wordpress.com/2014/12/19/los-numeros-de-feigenbaum/ Mahecha Zambrano, Daniel Felipe Martinez Ariza, Mauricio (2015-08-02) https://repository.urosario.edu.co/items/8b777db1-8130-43d1-8825-b349c5fe9a3f





